考点:异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:本题可以根据正方体的特征,把空间问题平面化,通过利用平行关系求的结果
解答:
解:
(1)如图所示:在正方体ABCD-A
1B
1C
1D
1中,CC
1∥BB
1∴异面直线AB
1与CC
1所成的角就是直线AB
1与直线BB
1所成的角
∴异面直线AB
1与CC
1所成的角为45°
(2)如图所示:在正方体ABCD-A
1B
1C
1D
1中,A
1B∥CD
1∴异面直线AB
1与CD
1所成的角就是直线AB
1与直线A
1B所成的角
∵AB
1⊥A
1B
∴异面直线AB
1与CD
1所成的角为90°
(3)如图所示:在正方体ABCD-A
1B
1C
1D
1中 A
1D∥B
1C
∴异面直线AB
1与A
1D所成的角就是直线AB
1与直线B
1C所成的角
连接AC
∵正方体的各个面都全等
∴AB
1=AC=B
1C
即△AB
1C为等边三角形
∴∠AB
1C=60°
异面直线AB
1与A
1D所成的角为60°
故答案为:45°、90°、60°
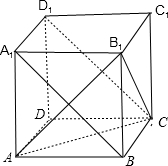
点评:本题重点考察的知识点:异面直线所成的角,可以利用平行关系,转化为求在同一平面内的直线所成的角




 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案