
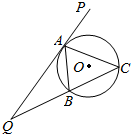
 如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,且QA为⊙O的切线
如图,△ABC的外接圆为⊙O,延长CB至Q,再延长QA至P,且QA为⊙O的切线分析 (1)由切线定理得QA2=QB•QC,由此能证明QC2-QA2=BC•QC.
(2)由弦切角定理和角平分线性质得QC2=QA2=15QC,△QCA∽△QAB,由此能求出QA的长度.
解答 证明:(1)∵QA为⊙O的切线,
∴QA2=QB•QC,
∵QC-QB=BC,
∴QC2-QA2=QC2-QB•QC=BC•QC.
解:(2)∵QA为⊙O的切线,∴∠PAC=∠ABC,
∵AC恰好为∠BAP的平分线,∴∠BAC=∠ABC,
∴AC=BC=15,
∴QC2=QA2=15QC,①
又由△QCA∽△QAB,得$\frac{QC}{QA}=\frac{AC}{AB}=\frac{15}{10}$,②
联合①②,消掉QC,得:QA=18.
点评 本题考查两线段平差等于两线段积的证明,考查线段长的求法,是中档题,解题时要认真审题,注意切线定理、弦切角定理的合理运用.


 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l⊥α,m⊥β,l⊥m⇒α⊥β | B. | l∥m,m⊆α⇒l∥α | ||
| C. | l⊆α,m⊆α,l∥β,m∥β⇒α∥β | D. | l⊥n,m⊥n⇒l∥m |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
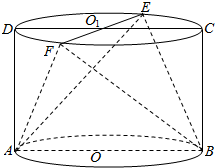 在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),AB=2,BC=$\sqrt{2}$.
在圆柱OO1中,ABCD是其轴截面,EF⊥CD于O1(如图所示),AB=2,BC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
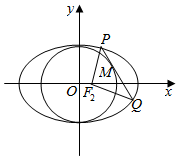 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点H(3,0)在椭圆上
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),点H(3,0)在椭圆上查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,|x|≥0 | B. | ?x∈R,|x|>0 | C. | ?x∈R,|x|≥0 | D. | ?x∈R,|x|<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
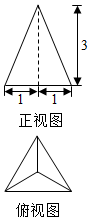
| A. | 6 | B. | $\frac{3\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{21}}{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com