
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)设h(x)=ax2-(2a+1)x+1+lnx,则问题等价于x∈(0,2]时,h(x)max≤0,通过讨论a的范围,根据函数的单调性确定a的具体范围即可.
解答 解:(1)g'(x)=-xsinx,∴g'(x)>0,即-xsinx>0,又x>0,
∴sinx<0,则2kπ+π<x<2kπ+2π(k≥0且k∈Z),
∴g'(x)<0,即-xsinx<0,又x>0,∴sinx>0,则2kπ<x<2kπ+π(k≥0且k∈Z),
所以函数g(x)的递增区间为(2kπ+π,2kπ+2π),递减区间为(2kπ,2kπ+π),其中(k≥0且k∈Z).
(2)f(x)=ax2-2ax+lnx,依题意得0<x≤2时,f(x)≤x-1,
即ax2-(2a+1)x+1+lnx≤0.
设h(x)=ax2-(2a+1)x+1+lnx,则问题等价于x∈(0,2]时,h(x)max≤0,
$h'(x)=2ax-(2a+1)+\frac{1}{x}=\frac{{2a{x^2}-(2a+1)x+1}}{x}=\frac{(x-1)(2ax-1)}{x}$.
(i)a≤0时,h'(1)=0;0<x<1时,h'(x)>0;
x>1时,h'(x)<0,∴h(x)max=h(1)=-a≤0,
∴a≥0,所以a=0,满足要求.
(ii)a>0时,$h'(x)=\frac{{2a(x-1)({x-\frac{1}{2a}})}}{x}$,
①$\frac{1}{2a}=1$,即$a=\frac{1}{2}$时,$h'(x)=\frac{{{{(x-1)}^2}}}{x}≥0$,h(x)在(0,+∞)上单调递增,
x∈(0,2]时,h(x)max=h(2)=-1+ln2<0,满足要求;
②$\frac{1}{2a}>1$,即$0<a<\frac{1}{2}$时,h(x)在(0,1)和$({\frac{1}{2a},\;\;+∞})上递增$,在$({1,\;\;\frac{1}{2a}})$上递减,
h(1)=-a<0,h(2)=-1+ln2<0,
∴x∈(0,2]时,h(x)max<0,满足要求;
③$0<\frac{1}{2a}<1$,即$a>\frac{1}{2}$时,h(x)在$({0,\;\;\frac{1}{2a}})$和(1,+∞)上递增,在$({\frac{1}{2a},\;\;1})$上递减.
$h({\frac{1}{2a}})=-\frac{1}{4a}+ln\frac{1}{2a}<0$,h(2)=-1+ln2<0,
∴x∈(0,2]时,h(x)max<0,满足要求,
综上得,存在实数a满足题意,a的取值范围为[0,+∞).
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,考查函数恒成立问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 50π | B. | 100π | C. | 200π | D. | $\frac{{125\sqrt{2}π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
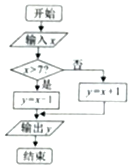 已知实数x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.
已知实数x的取值范围为[0,10],给出如图所示程序框图,输入一个数x.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$|+4|$\overrightarrow{b}$|=0 | B. | $\overrightarrow{a}$与$\overrightarrow{b}$是相反向量 | C. | $\overrightarrow{a}$与$\overrightarrow{b}$的方向相同 | D. | $\overrightarrow{a}$与$\overrightarrow{b}$的方向相反 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
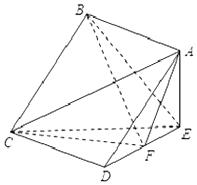 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com