练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$+4$\overrightarrow{b}$=0，则（　　）
    A．|$\overrightarrow{a}$|+4|$\overrightarrow{b}$|=0B．$\overrightarrow{a}$与$\overrightarrow{b}$是相反向量C．$\overrightarrow{a}$与$\overrightarrow{b}$的方向相同D．$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反

    分析 根据题意，由向量加法的运算性质可得$\overrightarrow{a}$=-4$\overrightarrow{b}$，即$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反，且|$\overrightarrow{a}$|=4|$\overrightarrow{b}$|，由此分析选项，即可得答案．

    解答 解：根据题意，非零向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$+4$\overrightarrow{b}$=0，
    即$\overrightarrow{a}$=-4$\overrightarrow{b}$，即$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反，且|$\overrightarrow{a}$|=4|$\overrightarrow{b}$|，
    依次分析选项：
    对于A：|$\overrightarrow{a}$|=4|$\overrightarrow{b}$|，|$\overrightarrow{a}$|+4|$\overrightarrow{b}$|=5|$\overrightarrow{b}$|≠0，故A错误；
    对于B：$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反，且|$\overrightarrow{a}$|=4|$\overrightarrow{b}$|，$\overrightarrow{a}$与$\overrightarrow{b}$的不是相反向量，故B错误；
    对于C：$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反，故C错误；
    对于D：$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反，D正确；
    故选：D．

    点评 本题考查平面的平行向量，关键是理解向量的基本定义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．为了得到函数$y=3sin（2x+\frac{π}{5}）$的图象，只需把y=3sin2x上的所有的点（　　）
    A．向左平行移动$\frac{π}{10}$长度单位B．向右平行移动$\frac{π}{10}$长度单位
    C．向右平行移动$\frac{π}{5}$长度单位D．向左平行移动$\frac{π}{5}$长度单位

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．执行如图所示的程序框图，若输入t的值为6，则输出的s的值为（　　）
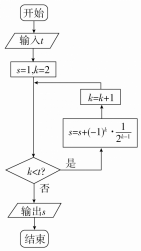
    A．$\frac{9}{16}$B．$\frac{5}{4}$C．$\frac{21}{16}$D．$\frac{11}{8}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．设关于x的一元二次方程x2+2ax+b2=0．
    （1）若a是从0，1，2，3，4五个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率；
    （2）若a是从区间[0，4]任取的一个数，b是从区间[1，4]任取的一个数，求上述方程有实根的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=ax2+bx+clnx（a，b，c∈R），g（x）=xcosx-sinx+1（x＞0）．
    （1）求函数g（x）的单调区间；
    （2）当b=-2a，c=1时，是否存在实数a，使得0＜x≤2时，函数y=f（x）图象上的点都在$\left\{\begin{array}{l}0＜x≤2\\ x-y-1≥0\end{array}\right.$所表示的平面区域内（含边界）？若存在，求出a的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知数列{an}是各项均为正数的等比数列，其前n项和为Sn，a1+a2=2，a5+a6=8，则S10=（　　）
    A．16B．32C．40D．62

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．A，B，C为△ABC的三个内角，下列关系中不成立的是（　　）
    ①cos（A+B）=cosC
    ②sin（2A+B+C）=sinA
    ③$cos\frac{B+C}{2}=sin\frac{A}{2}$
    ④tan（A+B）=-tanC．
    A．①②B．②③C．③④D．①④

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．（1）已知Z是复数，Z+2i，$\frac{Z}{2-i}$均为实数，且复数（Z+ai）2在复平面上对应的点在第一象限，求实数a的取值范围．
    （2）已知两个向量$\overrightarrow{a}$，$\overrightarrow{b}$对应的复数是z1=3和z2=-5+5i，求向量$\vec a$与$\vec b$的夹角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=ex-x+1
    （1）求函数y=f（x）在点（2，f（2））处的切线方程．
    （2）求函数y=f（x）在[-2，1]上的最大值和最小值．

    查看答案和解析>>

    同步练习册答案