
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
分析 利用三角形的内角和公式、诱导公式逐一判断各个选项中的式子是否成立,从而得出结论.
解答 解:对于①,∵角A,B,C是△ABC的三个内角,
∴A+B=π-C,
∴cos(A+B)=cos(π-C)=-cosC,故不成立;
对于②,由于sin(2A+B+C)=sin(π+A)=-sinA,故不成立;
对于③,∵cos$\frac{B+C}{2}$=cos($\frac{π}{2}$-$\frac{A}{2}$)=sin$\frac{A}{2}$,故成立;
对于④,tan(A+B)=tan(π-C)=-tanC.故成立.
故选:A.
点评 本题主要考查三角形的内角和公式、诱导公式的应用,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
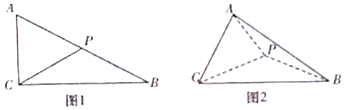 如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得AB=$\sqrt{10}$.
如图1,在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,P是AB边的中点,现把△ACP沿CP折成如图2所示的三棱锥A-BCP,使得AB=$\sqrt{10}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |$\overrightarrow{a}$|+4|$\overrightarrow{b}$|=0 | B. | $\overrightarrow{a}$与$\overrightarrow{b}$是相反向量 | C. | $\overrightarrow{a}$与$\overrightarrow{b}$的方向相同 | D. | $\overrightarrow{a}$与$\overrightarrow{b}$的方向相反 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
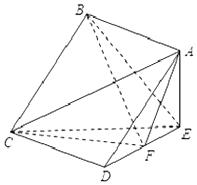 如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,AE⊥平面CDE,已知AE=DE=2,F为线段DE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{4}{5},+∞})$ | B. | $[{\frac{4}{5},+∞})$ | C. | $[{\frac{1}{3},+∞})$ | D. | (-∞,1)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com