
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 根据题意,先判断四边形ABCD是平行四边形,再判断平行四边形ABCD是菱形,求出它的面积即可.
解答 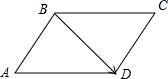 解:在四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{DC}$=(2,0),
解:在四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{DC}$=(2,0),
∴四边形ABCD是平行四边形;
又∵$\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}$=$\frac{\overrightarrow{BD}}{|\overrightarrow{BD}|}$,
∴平行四边形ABCD的角平分线BD平分∠ABC,
四边形ABCD是菱形,其边长为2,对角线BD等于2,
∴cos∠ABC=cos120°=-$\frac{1}{2}$,如图所示;
∴sin∠ABC=$\frac{\sqrt{3}}{2}$,
SABCD=2×$\frac{1}{2}$|$\overrightarrow{BA}$|•|$\overrightarrow{BC}$|•sin∠ABC=2×$\frac{1}{2}$×2×2×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$.
故选:A.
点评 本题考查了平面向量的应用问题,解题时应先判断四边形的形状,考查四边形面积的求法,属于中档题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 32 | C. | 40 | D. | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧(¬q) | B. | (¬p)∧q | C. | p∧q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{4}$ | B. | -4 | C. | 3 | D. | $-\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com