
分析 由$\overrightarrow{a}•\overrightarrow{b}=-|\overrightarrow{a}|•|\overrightarrow{b}|$便可得出$\overrightarrow{a},\overrightarrow{b}$的方向相反,即有$\overrightarrow{a}∥\overrightarrow{b}$,这样根据平行向量的坐标关系即可求出x值,并满足$\overrightarrow{a},\overrightarrow{b}$方向相反,从而确定x的值.
解答 解:$\overrightarrow{a}•\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=-1$;
∴$\overrightarrow{a},\overrightarrow{b}$夹角为π;
∴$\overrightarrow{a}∥\overrightarrow{b}$,且$\overrightarrow{a},\overrightarrow{b}$方向相反;
∴(x-1)2-4=0;
∴x-1=-2,或x-1=2(舍去);
∴x=-1.
故答案为:-1.
点评 考查向量数量积的计算公式,已知余弦值求角,向量夹角的概念,以及平行向量的坐标关系.


科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 1 | 3 | 6 | 7 | 8 |
| y | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x<y<z | B. | z<x<y | C. | z<y<x | D. | y<z<x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
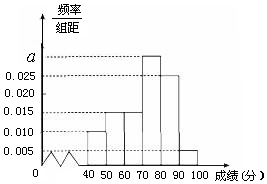 某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如图所示的部分频率分布直方图,请观察图形信息,回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com