
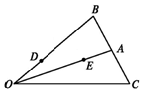
 已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近O的三等分点,设$\overrightarrow{OB}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$
已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近O的三等分点,设$\overrightarrow{OB}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$分析 (1)根据向量的三角形法则即可求出,
(2)根向量的三角形法则和向量的数乘运算可得$\overrightarrow{DE}$=$\frac{1}{6}$$\overrightarrow{BC}$,问题得以证明
解答 解:(1)$\overrightarrow{OA}$=$\frac{1}{2}$($\overrightarrow{OB}$+$\overrightarrow{OC}$)=$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$,
(2)证明:∵点D是线段OB的一个靠近B的三等分点,点E是线段OA靠近A的三等分点,
∴$\overrightarrow{OD}$=$\frac{1}{3}$$\overrightarrow{OB}$=$\frac{1}{3}$$\overrightarrow{a}$,$\overrightarrow{OE}$=$\frac{1}{3}$$\overrightarrow{OA}$=$\frac{1}{3}$($\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$)=$\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$,
∴$\overrightarrow{DE}$=$\overrightarrow{OE}$-$\overrightarrow{OD}$=-$\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$,
∵$\overrightarrow{BC}$=$\overrightarrow{OC}$-$\overrightarrow{OB}$=$\overrightarrow{b}$-$\overrightarrow{a}$,
∴$\overrightarrow{DE}$=$\frac{1}{6}$$\overrightarrow{BC}$,
∴$\overrightarrow{DE}$平行于$\overrightarrow{BC}$.
点评 本题考查的知识点是向量加减法的三角形法则和向量的共线定理,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 4:3:2 | B. | 2:3:4 | C. | $\frac{1}{4}$:$\frac{1}{3}$:$\frac{1}{2}$ | D. | $\frac{1}{2}$:$\frac{1}{3}$:$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
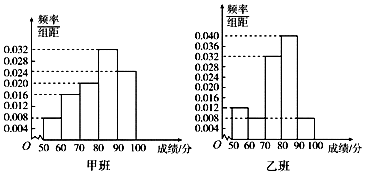
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | 12 | 4 | 20 |
| 成绩不优秀 | 38 | 46 | 80 |
| 总计 | 50 | 50 | 100 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数的最小正周期为$\frac{π}{4}$ | B. | 函数是偶函数 | ||
| C. | 函数图象的一条对称轴为$x=\frac{π}{3}$ | D. | 函数在$[{\frac{2π}{3},\frac{5π}{6}}]$上为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{6}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
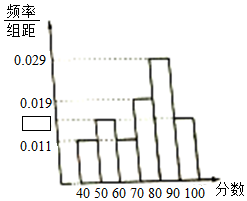 为了解某社区物业部门对本小区业主的服务情况,随机访问了100位业主,根据这100位业主对物业部门的评分情况,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].由于某种原因,有个数据出现污损,请根据图中其他数据分析,评分不小于80分的业主有( )位.
为了解某社区物业部门对本小区业主的服务情况,随机访问了100位业主,根据这100位业主对物业部门的评分情况,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].由于某种原因,有个数据出现污损,请根据图中其他数据分析,评分不小于80分的业主有( )位.| A. | 43 | B. | 44 | C. | 45 | D. | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com