
科目:高中数学 来源: 题型:解答题
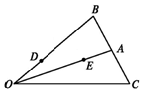 已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近O的三等分点,设$\overrightarrow{OB}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$
已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近O的三等分点,设$\overrightarrow{OB}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+3)2+(y-4)2=16 | B. | (x-3)2+(y+4)2=16 | C. | (x+3)2+(y-4)2=9 | D. | (x-3)2+(y+4)2=9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如下:根据学生体质健康标准,成绩不低于76的为优良.
某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如下:根据学生体质健康标准,成绩不低于76的为优良.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2017}{2}$ | B. | $\frac{2}{2017}$ | C. | $\frac{1}{2016}$ | D. | $\frac{1}{1008}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x-2 | B. | y=x+2 | C. | y=x-2(1≤x≤3) | D. | y=x+2(0≤y≤1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(b)<f(a)<f(c) | B. | f(c)<f(b)<f(a) | C. | f(c)<f(a)<f(b) | D. | f(b)<f(c)<f(a) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com