
分析 (1)由4Sn=an2+2an+1(n∈N*),n=1时,4a1=${a}_{1}^{2}$+2a1+1,解得a1=1.
n≥2时,4Sn-1=${a}_{n-1}^{2}$+2an-1+1,相减可得:(an+an-1)(an-an-1-2)=0,又an>0,可得an-an-1-2=0,利用等差数列的通项公式可得an.b1=a1=1,2b2,b4,3b3成等差数列.可得$2{b}_{2}{q}^{2}$=2b2+3b2q,化为:2q2-3q-2=0,q>1,解得q
(2)cn=$\frac{{a}_{n}}{{b}_{n}}$=$\frac{2n-1}{{2}^{n-1}}$.利用错位相减法、等比数列的求和公式即可得出.
解答 解:(1)由4Sn=an2+2an+1(n∈N*),n=1时,4a1=${a}_{1}^{2}$+2a1+1,解得a1=1.
n≥2时,4Sn-1=${a}_{n-1}^{2}$+2an-1+1,相减可得:4an=$({a}_{n}+1)^{2}$-$({a}_{n-1}+1)^{2}$,化为:(an+an-1)(an-an-1-2)=0,
又an>0,∴an-an-1-2=0,即an-an-1=2,
∴数列{an}是等差数列,公差为2.
∴an=1+2(n-1)=2n-1.
b1=a1=1,∵2b2,b4,3b3成等差数列.
∴2b4=2b2+3b3.∴$2{b}_{2}{q}^{2}$=2b2+3b2q,化为:2q2-3q-2=0,q>1,解得q=2.
∴bn=2n-1.
(2)证明:cn=$\frac{{a}_{n}}{{b}_{n}}$=$\frac{2n-1}{{2}^{n-1}}$.
{cn}的前项和为Tn=1+$\frac{3}{2}+\frac{5}{{2}^{2}}$+…+$\frac{2n-1}{{2}^{n-1}}$,
$\frac{1}{2}$Tn=$\frac{1}{2}+\frac{3}{{2}^{2}}$+…+$\frac{2n-3}{{2}^{n-1}}$+$\frac{2n-1}{{2}^{n}}$,
∴$\frac{1}{2}$Tn=1+2$(\frac{1}{2}+\frac{1}{{2}^{2}}+…+\frac{1}{{2}^{n-1}})$-$\frac{2n-1}{{2}^{n}}$=1+2×$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$-$\frac{2n-1}{{2}^{n}}$,
∴Tn=6-$\frac{2n+3}{{2}^{n-1}}$<6.
点评 本题考查了错位相减法、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:选择题
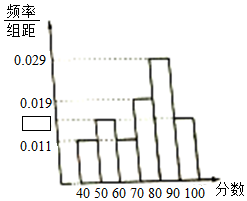 为了解某社区物业部门对本小区业主的服务情况,随机访问了100位业主,根据这100位业主对物业部门的评分情况,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].由于某种原因,有个数据出现污损,请根据图中其他数据分析,评分不小于80分的业主有( )位.
为了解某社区物业部门对本小区业主的服务情况,随机访问了100位业主,根据这100位业主对物业部门的评分情况,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100].由于某种原因,有个数据出现污损,请根据图中其他数据分析,评分不小于80分的业主有( )位.| A. | 43 | B. | 44 | C. | 45 | D. | 46 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
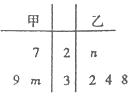 已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{7\sqrt{3}}{6}$ | C. | $\frac{\sqrt{21}}{3}$ | D. | $\frac{3\sqrt{3}}{4}$或$\frac{7\sqrt{3}}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com