
分析 (Ⅰ)直线y=x-1与x轴的交点坐标为(1,0),得椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的半焦距c.又离心率$e=\frac{c}{a}=\frac{1}{3}$,得a2=9,b2=8.即可求出椭圆方程.
(Ⅱ)设直线PQ的方程为y=kx+m(k<0,m>0),由$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{9}+\frac{y^2}{8}=1\end{array}\right.$得(8+9k2)x2+18kmx+9m2-72=0,利用根与系数的关系、弦长公式表示及直线PQ与圆x2+y2=8相切,表示出PQ,距离公式表示PF2,QF2由$|{P{F_2}}|+|{Q{F_2}}|+|{PQ}|=6-\frac{{{x_1}+{x_2}}}{3}-\frac{6km}{{8+9{k_2}}}$=$6+\frac{6km}{{8+9{k^2}}}-\frac{6km}{{8+9{k^2}}}=6$,即可求解.
解答 解:(Ⅰ)因为直线y=x-1与x轴的交点坐标为(1,0),由题意得椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的半焦距c=1.
又已知离心率$e=\frac{c}{a}=\frac{1}{3}$,所以a2=9,所以b2=8.
所以椭圆C的标准方程为$\frac{x^2}{9}+\frac{y^2}{8}=1$.
(Ⅱ)根据题意作出图形如图所示,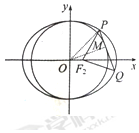
设直线PQ的方程为y=kx+m(k<0,m>0),
由$\left\{\begin{array}{l}y=kx+m\\ \frac{x^2}{9}+\frac{y^2}{8}=1\end{array}\right.$得(8+9k2)x2+18kmx+9m2-72=0,
所以△=(18km)2-4(8+9k2)(9m2-72)=288(9k2-m2+8)>0,
设P(x1,y1),Q(x2,y2),
则${x_1}+{x_2}=\frac{-18km}{{8+9{k^2}}},{x_1}{x_2}=\frac{{9{m^2}-72}}{{8+9{k^2}}}$,
所以$|{PQ}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|=\sqrt{1+{k^2}}\sqrt{{{({x_1}+{x_2})}^2}-4{x_1}{x_2}}$
=$\sqrt{1+{k^2}}\sqrt{(\frac{-18km}{{8+9{k^2}}})-4×\frac{{9{m^2}-72}}{{8+9{k^2}}}}$=$\sqrt{1+{k^2}}\sqrt{\frac{{4×9×8(9{k^2}-{m^2}+8)}}{{{{(8+9{k^2})}^2}}})}$,
因为直线PQ与圆x2+y2=8相切,所以$\frac{m}{{\sqrt{1+{k^2}}}}=2\sqrt{2}$,
即$m=\sqrt{8(1+{k^2})}$,所以$|{PQ}|=-\frac{6km}{{8+9{k^2}}}$,
因为$|{P{F_2}}|=\sqrt{{{({x_1}-1)}^2}+y_1^2}=\sqrt{{{({x_1}-1)}^2}+8(1-\frac{x_1^2}{9})}=\sqrt{{{(\frac{x_1}{3}-3)}^2}},0<{x_1}<3$,$|{P{F_2}}|=3-\frac{x_1}{3}$,
同理$|{Q{F_2}}|=3-\frac{x_2}{3}$(也可用焦半径公式),
所以$|{P{F_2}}|+|{Q{F_2}}|+|{PQ}|=6-\frac{{{x_1}+{x_2}}}{3}-\frac{6km}{{8+9{k_2}}}$=$6+\frac{6km}{{8+9{k^2}}}-\frac{6km}{{8+9{k^2}}}=6$
因此,△PF2Q的周长是定值,且定值为6.
点评 本题考查了椭圆的方程,椭圆与圆的切线的综合问题,同时考查了运算能力,属于难题.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 34种 | B. | 48种 | C. | 96种 | D. | 144种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
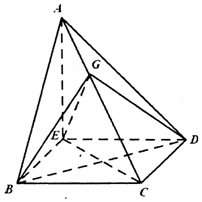 如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD.
如图,在三棱锥A-BCD中,∠ABC=∠BCD=∠CDA=90°,AC=6$\sqrt{3}$,BC=CD=6,E点在平面BCD内,EC=BD,EC⊥BD. 查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,2} | B. | {-1,2} | C. | $\{0,\frac{1}{2}\}$ | D. | $\{\frac{1}{2},2\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com