
| A. | $(-\frac{{6\sqrt{26}}}{13}\;,\;-2]∪[2\;,\;\frac{{6\sqrt{26}}}{13})$ | B. | $(-\frac{{6\sqrt{26}}}{13}\;,\;-2)∪(2\;,\;\frac{{6\sqrt{26}}}{13})$ | ||
| C. | $(-2\sqrt{2}\;,\;-2]∪[2\;,\;2\sqrt{2})$ | D. | $(-2\sqrt{2}\;,\;-2)∪(2\;,\;2\sqrt{2}]$ |
分析 由点P满足双曲线方程,由B1(0,3),B2(0,-3),运用向量的数量积的坐标表示,解不等式即可得到所求范围.
解答 解:由题意可得9x02-4y02=36,
可得y02=$\frac{9}{4}$x02-9,
B1(0,3),B2(0,-3),
由$\overrightarrow{P{B_1}}•\overrightarrow{P{B_2}}$<8,可得(-x0,3-y0)•(-x0,-3-y0)<8,
即x02+y02-9<8,
可得$\frac{13}{4}$x02-26<0,
解得-2$\sqrt{2}$<x0<2$\sqrt{2}$,
由x0≥2或x0≤-2,
可得-2$\sqrt{2}$<x0≤-2或2≤x0<2$\sqrt{2}$.
故选:C.
点评 本题考查点满足双曲线的方程,以及向量的数量积的坐标表示,考查不等式的解法,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{8}$ | B. | $\frac{\sqrt{10}}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
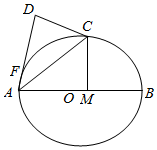 如图,AB是圆O的直径,C,F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C,且交AF的延长线于点D,CM⊥AB,垂足为点M.
如图,AB是圆O的直径,C,F为圆O上的点,CA是∠BAF的角平分线,CD与圆O切于点C,且交AF的延长线于点D,CM⊥AB,垂足为点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
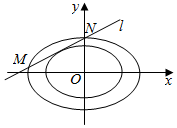 如图,已知椭圆C的中心在原点O,左焦点为F1(-1,0),左顶点为A,且F1为AO的中点.
如图,已知椭圆C的中心在原点O,左焦点为F1(-1,0),左顶点为A,且F1为AO的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com