
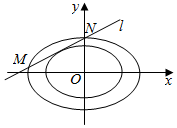
 如图,已知椭圆C的中心在原点O,左焦点为F1(-1,0),左顶点为A,且F1为AO的中点.
如图,已知椭圆C的中心在原点O,左焦点为F1(-1,0),左顶点为A,且F1为AO的中点.分析 (1)由椭圆C的中心在原点O,左焦点为F1(-1,0),左顶点为A,且F1为AO的中点,求出a,b,c,由此能求出椭圆C的方程.
(2)椭圆C1的3倍相似椭圆C2的方程为:$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{9}=1$.切线m垂直于x轴,则其方程为:x=±2,推导出|MN|=2$\sqrt{6}$;若切线m不垂直于x轴,可设其方程为:y=kx+b,代入椭圆C1方程,得(3+4k2)x2+8kbx+4b2-12=0,由此利用根的判别式、韦达定理、弦长公式,结合已知条件能求出弦长|MN|的最大值.
解答 解:(1)∵椭圆C的中心在原点O,左焦点为F1(-1,0),左顶点为A,且F1为AO的中点,
∴c=1,a=2,∴b2=4-1=3,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)椭圆C1的3倍相似椭圆C2的方程为:$\frac{{x}^{2}}{12}+\frac{{y}^{2}}{9}=1$.
①若切线m垂直于x轴,则其方程为:x=±2,解得y=$±\sqrt{6}$,
∴|MN|=2$\sqrt{6}$.
②若切线m不垂直于x轴,可设其方程为:y=kx+b.
将y=kx+b代入椭圆C1方程,得:(3+4k2)x2+8kbx+4b2-12=0,
△=(8kb)2-4(3+4k2)(4b2-12)=48(4k2+3-b2)=0,
即b2=4k2+3,(*),
设M,N两点的坐标分别是(x1,y1),(x2,y2),
将y=kx+b代入椭圆C2的方程,得:(3+4k2)x2+8kbx+4b2-36=0,
此时,${x}_{1}+{x}_{2}=-\frac{8kb}{3+4{k}^{2}}$,x1x2=$\frac{4{b}^{2}-36}{3+4{k}^{2}}$,
∴|x1-x2|=$\frac{4\sqrt{3(12{k}^{2}+9-{b}^{2})}}{3+4{k}^{2}}$,
∴|MN|=$\sqrt{1+{k}^{2}}$×$\frac{4\sqrt{3(12{k}^{2}+9-{b}^{2})}}{3+4{k}^{2}}$=4$\sqrt{6}$$\sqrt{\frac{1+{k}^{2}}{3+4{k}^{2}}}$=2$\sqrt{6}$$\sqrt{1+\frac{1}{3+4{k}^{2}}}$,
∵3+4k2≥3,∴1<1+$\frac{1}{3+4{k}^{2}}$$≤\frac{4}{3}$,即2$\sqrt{6}$<2$\sqrt{6}$$\sqrt{1+\frac{1}{3+4{k}^{2}}}$≤4$\sqrt{2}$,
综合①②,得弦长|MN|的取值范围是[2$\sqrt{6}$,4$\sqrt{2}$],
∴弦长|MN|的最大值是4$\sqrt{2}$.
点评 本题考查椭圆方程的求法,考查弦长的最大值的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、弦长公式的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{{6\sqrt{26}}}{13}\;,\;-2]∪[2\;,\;\frac{{6\sqrt{26}}}{13})$ | B. | $(-\frac{{6\sqrt{26}}}{13}\;,\;-2)∪(2\;,\;\frac{{6\sqrt{26}}}{13})$ | ||
| C. | $(-2\sqrt{2}\;,\;-2]∪[2\;,\;2\sqrt{2})$ | D. | $(-2\sqrt{2}\;,\;-2)∪(2\;,\;2\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com