
���� �ٸ��ݸ����ļ��������Լ������ľ��빫ʽ�����жϣ�
�ڸ��ݻ�������ʽ���������������жϣ�
�۸��������ľ����Լ������εı߳���ϵ�����жϣ�
�ܸ��ݺ���ͼ��֮��Ĺ�ϵ�����жϣ�
��� �⣺��|z+i|��ʾ��ƽ���ϣ���z���B��0��-1���ľ��룬|z-i|��ʾ��ƽ���ϣ���Z���A��0��1���ľ��룬
��|z+i|+|z-i|=2����ʾ��ƽ���ϣ���z���A��B�ľ���֮�͵���2�����Ӧ��Ĺ켣���߶Σ��ʢٴ���
�ڵ�x��0��x��1ʱ����x��1��lnx+$\frac{1}{lnx}$��2����0��x��1����lnx+$\frac{1}{lnx}$��-2���ʢڴ���
��P��x��y����x��0��y��0����C�ϵĶ�������$C��\sqrt{\frac{x^2}{9}}-\sqrt{\frac{y^2}{16}}=1$����$\frac{x}{3}-\frac{y}{4}=1$��x��0��y��0��
������������E��-5��0����F��5��0������P��E��F����λ����ͼʾ��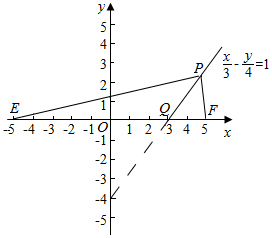
��y=0ʱ��P����Q���غϣ���||PE|-|PF||=||QE|-|QF||=6��
��y��0��||PE|-|PF||��|EF|=10�����ʢܴ���
�ܺ���y=2+logax��ͼ������к���y=logax������a��0��a��1����ͼ��ͨ������ƽ�Ƶõ��ģ��ʢܴ���
�ʴ��������Ǣ٢ڢۢܣ�
�ʴ�Ϊ���٢ڢۢ�
���� ������Ҫ�������������жϣ��漰��֪ʶ��϶࣬�ۺ��Խ�ǿ����һ�����Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | i | B�� | -i | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 25�� | B�� | 12.5�� | C�� | 22�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
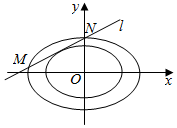 ��ͼ����֪��ԲC��������ԭ��O����ΪF1��-1��0������ΪA����F1ΪAO���е㣮
��ͼ����֪��ԲC��������ԭ��O����ΪF1��-1��0������ΪA����F1ΪAO���е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com