
分析 (1)求函数的导数,根据导数的几何意义即可求出函的切线斜率,即可求得a的值;
(2)求导数,构造辅助函数g(x)=lnx+$\frac{1}{x}$+1-a,求导,令g′(x)=0,求得g(x)的最小值,判断f′(x)≥0,可判断函数的单调性;
(3)由(2)知f(x)在(1,2)上是增函数,可知(x+1)lnx>2(x-1),即$\frac{1}{lnx}$<$\frac{x+1}{2(x-1)}$利用函数的单调性,求得-$\frac{1}{ln(2-x)}$<$\frac{3-x}{2(x-1)}$,根据对数函数的运算即可证明不等式成.
解答 解:(1)f′(x)=lnx+$\frac{1}{x}$+1-a,x∈(0,+∞)
由题意可知:$\frac{f(e)-f(2-e)}{e-0}$=f′(e),
整理得:e+1-a(e-1)-(2-e)=e(1+$\frac{1}{e}$+1-a),解得a=2;
(2))f′(x)=lnx+$\frac{1}{x}$+1-a,记g(x)=lnx+$\frac{1}{x}$+1-a,
g′(x)=$\frac{x-1}{{x}^{2}}$,令g′(x)=0,x=1,
∴g(x)min=g(1)=2-a,
∵a≤2,
∴2-a≥0,
∴g(x)≥g(1)=0,f′(x)≥0,
∴函数f(x)的定义域上为增函数;
(3)证明:由(2)知当a=2时,f(x)在(1,2)上是增函数,
∴f(x)>f(1)=0,即(x+1)lnx>2(x-1),
∴$\frac{1}{lnx}$<$\frac{x+1}{2(x-1)}$,①
∵1<x<2,
∴0<2-a<1,$\frac{1}{2-x}>1$,
∴$\frac{1}{ln\frac{1}{2-x}}$<$\frac{\frac{1}{2-x}+1}{2(\frac{1}{2-x}-1)}$=$\frac{3-x}{2(x-1)}$,
即-$\frac{1}{ln(2-x)}$<$\frac{3-x}{2(x-1)}$,②
①+②得:$\frac{1}{lnx}$-$\frac{1}{ln(2-x)}$<$\frac{x+1}{2(x-1)}$+$\frac{3-x}{2(x-1)}$=$\frac{2}{x-1}$
∴原式成立.
点评 本题考查运用导数思想求切线的斜率、单调区间和极值,同时考查构造函数求导数,判断单调性,运用单调性证明不等式,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
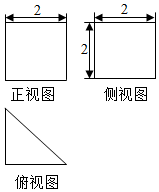
| A. | 1:3π | B. | $\sqrt{3}:π$ | C. | $1:3\sqrt{3}π$ | D. | $1:\sqrt{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 2$\sqrt{10}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
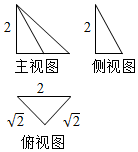
| A. | 8π | B. | 4π | C. | $\frac{8\sqrt{2}π}{3}$ | D. | $\frac{4\sqrt{2}π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com