Question

19．正三棱锥P-ABC，侧棱长与底面边长相等，F是BC的中点，异面直线AC与PF所成的角为arccos$\frac{\sqrt{3}}{6}$．

Answer 1

分析 作SO⊥底面ABC，交平面ABCD于点O，取AB中点E，取BC中点F，以O为原点，OE为x轴，OF为y轴，OS为z轴，建立空间直角坐标系，利用向量法能求出异面直线AC与PF所成的角．

解答 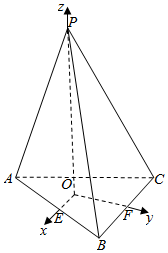解：作SO⊥底面ABC，交平面ABCD于点O，取AB中点E，取BC中点F
以O为原点，OE为x轴，OF为y轴，OS为z轴，建立空间直角坐标系，
设AB=BC=AC=SA=SB=SC=2，
则A（0，-$\frac{2\sqrt{3}}{3}$，0），C（-1，$\frac{\sqrt{3}}{3}$，0），
P（0，0，$\frac{2\sqrt{6}}{3}$），F（0，$\frac{\sqrt{3}}{3}$，0），
$\overrightarrow{AC}$=（-1，$\sqrt{3}$，0），$\overrightarrow{PF}$=（0，$\frac{\sqrt{3}}{3}$，-$\frac{2\sqrt{6}}{3}$），
设异面直线AC与PF所成的角为θ，
则cosθ=$\frac{|\overrightarrow{AC}•\overrightarrow{PF}|}{|\overrightarrow{AC}|•|\overrightarrow{PF}|}$=$\frac{1}{2\sqrt{3}}$=$\frac{\sqrt{3}}{6}$．
∴θ=arccos$\frac{\sqrt{3}}{6}$．
∴异面直线AC与PF所成的角为arccos$\frac{\sqrt{3}}{6}$．

点评 本题考查异面直线所成角的求法，是中档题，解题时要认真审题，注意向量法的合理运用．