
分析 (1)求出幂函数的解析式以及一次函数的解析式,化简函数f(x),然后求解单调区间.
(2)利用偶函数求出μ,求出最小值a,求出函数的最大值的表达式,然后再求解最大值的表达式的最小值.
(3)利用已知条件,转化求出b的范围,然后通过基本不等式以及函数的最值,通过分类讨论求解即可.
解答 解:(1)幂函数f1(x)的图象过点(2,$\sqrt{2}$),可得$\sqrt{2}={2}^{a}$,a=$\frac{1}{2}$.f1(x)=$\sqrt{x}$,函数f2(x)=1.
函数f(x)=|$\sqrt{x}$-1|=$\left\{\begin{array}{l}\sqrt{x}-1,x≥1\\ 1-\sqrt{x},0≤x<1\end{array}\right.$,函数的单调增区间为:[1,+∞),单调减区间:[0,1).
(2)y=log4[($\frac{1}{2}$)x+μ•2x]是偶函数,可得log4[($\frac{1}{2}$)x+μ•2x]=log4[($\frac{1}{2}$)-x+μ•2-x],
可得μ=1.
∴y=log4[($\frac{1}{2}$)x+2x],($\frac{1}{2}$)x+2x≥2,当且仅当x=0,函数取得最小值a=$\frac{1}{2}$.f1(x)=$\sqrt{x}$,函数f2(x)=$\frac{1}{2}x$+b.函数f(x)=|f1(x)-f2(x)|=|$\sqrt{x}$$-\frac{1}{2}x$-b|,x∈[0,4],
令h(x)=$\sqrt{x}$$-\frac{1}{2}x$-b,x∈[0,4],h′(x)=$\frac{1}{2\sqrt{x}}-\frac{1}{2}$,令$\frac{1}{2\sqrt{x}}-\frac{1}{2}$=0,解得x=1,当x∈(0,1)时,h′(x)>0
函数是增函数,当x∈(1,4)时,h′(x)<0,函数是减函数.
h(x)的极大值为:h(1)=$\frac{1}{2}-b$,最小值为h(0)=h(4)=-b,
函数f(x)在[0,4]上的最大值为u(b)=$\left\{\begin{array}{l}b,b>\frac{1}{4}\\ \frac{1}{2}-b,b≤\frac{1}{4}\end{array}\right.$,
函数u(b)的最小值:$\frac{1}{4}$.
(3)对于任意x∈[0,1],均有|f2(x)|≤1,即对于任意x∈[0,1],均有|ax+b|≤1,
当a>0时,显然b≥1不成立,
①当1>b≥0时,对于任意x∈[0,1],均有|ax+b|≤1,0≤a≤1,
可得0<a+b≤1,则(a+1)(b+1)≤$({\frac{a+1+b+1}{2})}^{2}$≤$\frac{9}{4}$,此时a=b=$\frac{1}{2}$.
(a+1)(b+1)∈[1,$\frac{9}{4}$].
②b∈[-$\frac{1}{2}$,0),对于任意x∈[0,1],均有|ax+b|≤1,
转化为:0≤a+b≤1,则(a+1)(b+1)∈[$\frac{3}{4}$,2),a=1,b=0时(a+1)(b+1)取最大值2.a=$\frac{1}{2}$,b=-$\frac{1}{2}$
,(a+1)(b+1)取得最小值$\frac{3}{4}$.
③b∈[-1,-$\frac{1}{2}$),对于任意x∈[0,1],均有|ax+b|≤1,
转化为:x=0,|b|≤1恒成立.-1<a+b≤1,
(a+1)>0,(b+1)>0,则(a+1)(b+1)≤$({\frac{a+1+b+1}{2})}^{2}$,$\frac{1}{4}$≤$({\frac{a+1+b+1}{2})}^{2}$≤$\frac{9}{4}$,
则(a+1)(b+1)∈[$\frac{1}{4}$,$\frac{9}{4}$],
④当b<-1时,对于任意x∈[0,1],|ax+b|≤1,不恒成立.
当a=0时,可得|b|≤1,(a+1)(b+1)∈[0,2].
当a<0时,如果|b|>1,对于任意x∈[0,1],不恒有|ax+b|≤1,
则|b|≤1,当0≤b≤1时,a∈[-1,0)对于任意x∈[0,1],均有|ax+b|≤1,
a+1∈[0,1),b+1∈[1,2].(a+1)(b+1)∈[0,2).
-1<b<0,可得|a+b|≤1.可得-1≤a+b≤1,a+1∈[0,1),b+1∈(0,1).
(a+1)(b+1)∈(0,1).
综上:代数式(a+1)(b+1)的取值范围:[0,$\frac{9}{4}$].
点评 本题考查函数的导数的综合应用,函数的最值,分类讨论以及转化思想的应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
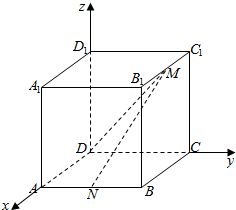 在长方体ABCD-A1B1C1D1中,|AB|=|BC|=2,|D1D|=3,点M是B1C1的中点,点N是AB的中点.建立如图所示的空间直角坐标系.
在长方体ABCD-A1B1C1D1中,|AB|=|BC|=2,|D1D|=3,点M是B1C1的中点,点N是AB的中点.建立如图所示的空间直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
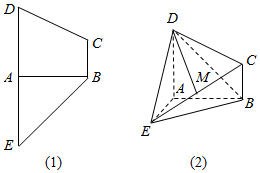
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
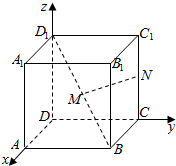 如图所示,建立空间直角坐标系Dxyz,已知正方体ABCD-A1B1C1D1的棱长为1,点M是正方体对角线D1B的中点,点N在棱CC1上.
如图所示,建立空间直角坐标系Dxyz,已知正方体ABCD-A1B1C1D1的棱长为1,点M是正方体对角线D1B的中点,点N在棱CC1上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
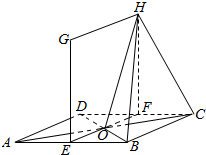 如图,菱形ABCD中,∠BAD=60°,边长AB=2,GE⊥平面ABCD,EF⊥ABCD,E,F分别是边AB、CD中点,AC与BD交于O,EG=FH=2,
如图,菱形ABCD中,∠BAD=60°,边长AB=2,GE⊥平面ABCD,EF⊥ABCD,E,F分别是边AB、CD中点,AC与BD交于O,EG=FH=2,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com