
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
分析 先根据题意画出区域,然后依据图形得到积分下限为0,积分上限为1,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可
解答 解:由题意封闭图形如图, 得到积分上限为1,积分下限为0
得到积分上限为1,积分下限为0
直线y=x与曲线y=x2所围图形的面积S=∫01(x-x2)dx
而∫01(x-x2)dx=($\frac{1}{2}$x2-$\frac{1}{3}$x3)|${\;}_{0}^{1}$=$\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$;
∴曲边梯形的面积是$\frac{1}{6}$;
故选:D.
点评 本题主要考查了学生会求出原函数的能力,以及考查了数形结合的思想,同时会利用定积分求图形面积的能力,解题的关键就是求原函数


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题

| A. | i<4 | B. | i<5 | C. | i≥5 | D. | i<6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{21}$ | B. | 21 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
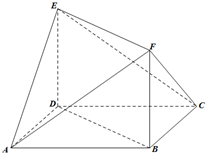 如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,
如图,多面体ABCDEF中,DE⊥平面ABCD,底面ABCD是菱形,AB=2,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-8,8) | B. | (8,8) | C. | (-8,-8)或(8,-8) | D. | (-8,8)或(8,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
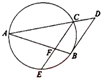 如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.
如图,已知AB和AC是圆的两条弦,过点B作圆的切线与AC的延长线相交于D.过点C作BD的平行线与圆交于点E,与AB相交于点F,AF=4,FB=1,EF=2,则线段AC的长为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com