练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知y＝f(x)是定义在R上的奇函数，且x＜0时，f(x)＝1＋2x.

    (1)求函数f(x)的解析式；

    (2)画出函数f(x)的图象；

    (3)写出函数f(x)单调区间及值域．


    [解析]　(1)因为y＝f(x)是定义在R上的奇函数，

    所以f(0)＝－f(0)，所以f(0)＝0，

    因为x＜0时，f(x)＝1＋2x，

    所以x＞0时，f(x)＝－f(－x)＝－(1＋2－x)＝－1－，

    所以f(x)＝

    (2)函数f(x)的图象为

    (3)根据f(x)的图象知：

    f(x)的单调增区间为(－∞，0)，(0，＋∞)；

    值域为{y|1＜y＜2或－2＜y＜－1或y＝0}．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    猎人在相距100 m处射击一野兔，命中的概率为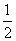，如果第一次未击中，则猎人进行第二次射击，但距离已是150 m，如果又未击中，则猎人进行第三次射击，但距离已是200 m，已知此猎人命中的概率与距离的平方成反比，求射击不超过三次击中野兔的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    把[0,1]内的均匀随机数分别转化为[0,4]和[－4,1]内的均匀随机数，需实施的变换分别为(　　)

    A．y＝－4x，y＝5－4                  B．y＝4x－4，y＝4x＋3

    C．y＝4x，y＝5x－4                   D．y＝4x，y＝4x＋3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若f(x)＝是R上的单调递增函数，则实数a的取值范围是(　　)

    A．(1，＋∞)                         B．[4,8)

    C．(4,8)                             D．(1,8)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知指数函数f(x)＝ax(a＞0，且a≠1)，

    (1)求f(0)的值；

    (2)如果f(2)＝9，求实数a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知A＝B＝R，x∈A，y∈B，f：x→y＝ax＋b是从A到B的映射，若1和8的原像分别是3和10，则5在f作用下的像是(　　)

    A．3                                   B．4

    C．5                                   D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    将二次函数y＝x2＋1的图像向左平移2个单位，再向下平移3个单位，所得二次函数的解析式是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用二分法求方程f(x)＝0在区间(1,2)内的唯一实数解x0时，经计算得f(1)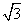＝，f(2)＝－5，f(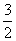)＝9，则下列结论正确的是(　　)

    A．x0∈(1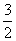，)                       B．x0＝－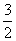

    C．x0∈(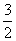，2)                       D．x0＝1

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)＝x3－2x2＋2x的零点个数为(　　)

    A．0                                   B．1

    C．2                                   D．3

    查看答案和解析>>

    同步练习册答案