
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 根据诱导公式、两角和的正弦函数、角之间的关系化简函数y的解析式,由正弦函数的最大值求出此函数的最大值.
解答 解:由题意得,y=sin(x+17°)-sin(x+257°)
=sin(x+17°)-sin(180°+x+77°)
=sin(x+17°)+sin[60°+(x+17°)]
=sin(x+17°)+$\frac{\sqrt{3}}{2}$cos(x+17°)+$\frac{1}{2}$sin(x+17°)
=$\frac{3}{2}$sin(x+17°)+$\frac{\sqrt{3}}{2}$cos(x+17°)
=$\sqrt{3}$[$\frac{\sqrt{3}}{2}$sin(x+17°)+$\frac{1}{2}$cos(x+17°)]
=$\sqrt{3}sin(x+17°+30°)$=$\sqrt{3}sin(x+47°)$
因为sin(x+47°)的最大值是1,所以函数y的最大值是$\sqrt{3}$,
故选:D.
点评 本题考查正弦函数的最值,诱导公式、两角和的正弦函数,以及变角在化简中的应用,考查化简、变形能力.


科目:高中数学 来源: 题型:解答题
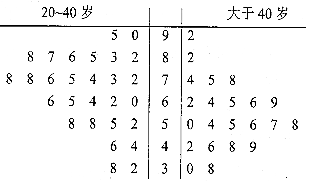
| 购买意愿强 | 购买意愿弱 | 合计 | |
| 20-40岁 | |||
| 大于40岁 | |||
| 合计 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
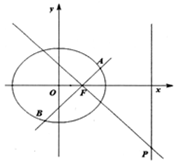 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-1}]∪[{\frac{2}{3},+∞})$ | B. | $({-∞,-1}]∪[{\frac{1}{2},+∞})$ | C. | $({-∞,-\frac{1}{2}}]∪[{\frac{1}{3},+∞})$ | D. | $({-∞,-\frac{1}{2}}]∪[{\frac{1}{6},+∞})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com