练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．若变量x，y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{y-x≤1}\\{x≤1}\end{array}\right.$，则$\frac{y+1}{x}$的最小值是（　　）
    A．0B．1C．-1D．3

    分析 首先画出可行域，利用$\frac{y+1}{x}$的几何意义是过区域内的点与定点（0，-1）连接的直线的斜率解答即可．

    解答 解：画出的可行域如图：
    目标函数的几何意义是过区域内的点与定点（0，-1）
    连接的直线中，
    斜率最小值，由其几何意义得到与（1，0）连接的直线斜率最小，
    所以最小值为$\frac{1-0}{0-（-1）}=1$；
    故选B．

    点评 本题考查了可行域的画法以及利用目标函数的几何意义求最值；本题解答的关键是明确目标函数的几何意义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届湖南永州市高三高考一模考试数学（文）试卷（解析版） 题型：选择题

    在中，是角的对边，，，则（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在△ABC中，角A、B、C的对边分别为a、b、c，且满足asinC=$\sqrt{3}$ccosA．
    （Ⅰ） 求角A的大小；
    （Ⅱ） 若△ABC面积S=5$\sqrt{3}$，b=5，求sinBsinC的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

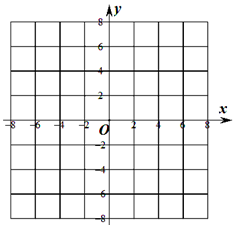    16．设f（x）=$\left\{{\begin{array}{l}{x+2（x≤-1）}\\{{x^2}（-1＜x＜2）}\\{2x（x≥2）}\end{array}}$，
    （1）在下列直角坐标系中画出f（x）的图象；
    （2）若f（x）=3，求x的值；
    （3）看图象写出函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源：2017届湖南永州市高三高考一模考试数学（文）试卷（解析版） 题型：选择题

    某学校高一、高二、高三年级的学生人数之比为4:3:3，现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本，则从高二年级抽取的学生人数为（ ）

    A．15 B．20 C．25 D．30

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．在同一坐标系内，函数y=xa（a≠0）和y=ax+$\frac{1}{a}$的图象应是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．若“x＞a”是“x＞2”的充分不必要条件，则实数a的取值范围为（2，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．若函数f（x）=（${\frac{1}{2}}$）|1-x|+m有零点，则m的取值范围是-1≤m＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

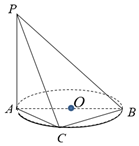    14．如图，AB是⊙O的直径，P是⊙O所在平面外一点，PA垂直于⊙O所在平面，且PA=AB=10，设点C为⊙O上异于A、B的任意一点．
    （1）求证：BC⊥平面PAC；
    （2）若AC=6，求三棱锥C-PAB的体积．

    查看答案和解析>>

    同步练习册答案