
分析 (Ⅰ)当a=2时,P(2,2)或P(2,-2),由此能出过点P的圆C2的切线方程;
(Ⅱ)设P=(a,b)=($\frac{{t}^{2}}{2}$,t),t≥2,A(1,0),由题意得PE=$\frac{{t}^{2}}{2}$,S△PBC=$\frac{1}{2}$BC×P横坐标=$\frac{1}{4}$BC×t2,求出BC=$\frac{2{t}^{2}}{{t}^{2}-4}$,设m=t2-4,利用均值定理能求出△PBC的面积的最小值.
解答 解:(Ⅰ)当a=2时,b2=2×2=4,解得b=±2,
∴P(2,2)或P(2,-2),
当P(2,2)时,设过点P的圆C2的切线方程为y-2=k(x-2),
即kx-y-2k+2=0,
圆C2:(x-1)2+y2=1的圆心C2(1,0),半径r=1,
∴$\frac{|k-2k+2|}{\sqrt{{k}^{2}+1}}$=1,解得k=$\frac{3}{4}$,
∴过点P的圆C2的切线方程为y-2=$\frac{3}{4}$(x-2),即3x-4y+2=0,
当切线斜率不存在时,所求的切线为x=2,成立;
当P(2,-2)时,设过点P的圆C2的切线方程为y+2=k(x-2),即kx-y-2k-2=0,
圆C2:(x-1)2+y2=1的圆心C2(1,0),半径r=1,
∴$\frac{|k-2k-2|}{\sqrt{{k}^{2}+1}}$=1,解得k=-$\frac{3}{4}$,
∴过点P的圆C2的切线方程为y+2=-$\frac{3}{4}$(x-2),即3x+4y+14=0,
当切线斜率不存在时,所求的切线为x=2,成立.
∴过点P(2,2)的圆C2的切线方程为3x-4y+2=0和x=2.
过点P(2,-2)的圆C2的切线方程为3x+4y+14=0和x=2.
(Ⅱ)设P=(a,b)=($\frac{{t}^{2}}{2}$,t),t≥2,A(1,0),
由题意得:PE=$\sqrt{P{A}^{2}-1}$=$\sqrt{(\frac{{t}^{2}}{2}-1)^{2}+{t}^{2}-1}$=$\frac{{t}^{2}}{2}$,
由切线长知识PE=PF,BO=BE,CO=CF,
∴S△PBC=$\frac{1}{2}$BC×P横坐标=$\frac{1}{4}$BC×t2,
又S△PBC=$\frac{1}{2}$(BO+CO+BE+CF+PE+PF)r=$\frac{1}{2}$(2BC+2PE)r=BC+$\frac{1}{2}$t2,
∴$\frac{1}{4}$BC×t2=BC+$\frac{1}{2}$t2,
解得:BC=$\frac{2{t}^{2}}{{t}^{2}-4}$,
设m=t2-4,
则S△PBC=$\frac{1}{2}$BC×P横坐标=$\frac{1}{4}$×$\frac{2{t}^{2}}{{t}^{2}-4}$×t2=$\frac{1}{2}×\frac{(m+4)^{2}}{m}$=$\frac{1}{2}(m+\frac{16}{m}+8)$
≥$\frac{1}{2}×(2\sqrt{m×\frac{16}{m}}+8)$=8.
当且仅当m=4,即a=2时,△PBC的面积取最小值8.
点评 本题考查切线方程的求法,考查三角形面积最小值的求法,是中档题,解题时要认真审题,注意圆的性质、切线方程的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
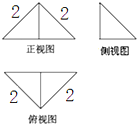 把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )
把边长为2的正方形ABCD沿对角线BD折起,形成的三棱锥A-BCD的三视图如图所示,则这个三棱锥的表面积为( )| A. | 2$\sqrt{3}$+4 | B. | 4$\sqrt{3}$ | C. | 8 | D. | 2$\sqrt{3}$+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 根据最新修订的《环境空气质量标准》指出空气质量指数在0~50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.
根据最新修订的《环境空气质量标准》指出空气质量指数在0~50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{e_1}$,2$\overrightarrow{e_2}$ | B. | $\overrightarrow{e_1}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ | ||
| C. | -$\overrightarrow{e_1}+\overrightarrow{e_2}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ | D. | $\overrightarrow{e_1}+\overrightarrow{e_2}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,四棱锥P-ABCD中,ABCD是边长为2的菱形,且∠BAD=60°,PA⊥PC,
如图,四棱锥P-ABCD中,ABCD是边长为2的菱形,且∠BAD=60°,PA⊥PC,| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 S(1,1)是抛物线L:y2=2px(p>0)上一点,以S为圆心,r为半径的圆,与x轴正半轴相交于A,B两点,连结并延长SA,SB,分别交椭圆L于C,D两点(如图所示).
S(1,1)是抛物线L:y2=2px(p>0)上一点,以S为圆心,r为半径的圆,与x轴正半轴相交于A,B两点,连结并延长SA,SB,分别交椭圆L于C,D两点(如图所示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com