
分析 (Ⅰ)利用同角三角函数的关系消元得到圆C的方程,将直线l的参数方程左侧展开,利用极坐标与直角坐标的对应关系得出直线l的直角坐标方程;
(Ⅱ)先求点M(x,y)到直线AB:x-y+2=0的距离为d=$\frac{|2cosθ-2sinθ+9|}{\sqrt{2}}$,再求△ABM的面积S=$\frac{1}{2}×|AB|×d$=|2cos$θ-2sinθ+9|=|2\sqrt{2}$sin$(\frac{π}{4}-θ)$+9|,然后求最值.
解答 解:(1)圆C的参数方程为$\left\{\begin{array}{l}{x=3+2cosθ}\\{y=-4+2sinθ}\end{array}\right.$(θ为参数).
所以普通方程为(x-3)2+(y+4)2=4.
∴圆C的极坐标方程:ρ2-6ρcosθ+8ρsinθ+21=0.
(2)点M(x,y)到直线AB:x-y+2=0的距离为d=$\frac{|2cosθ-2sinθ+9|}{\sqrt{2}}$,
△ABM的面积S=$\frac{1}{2}×|AB|×d$=|2cos$θ-2sinθ+9|=|2\sqrt{2}$sin$(\frac{π}{4}-θ)$+9|
所以△ABM面积的最大值为9+2$\sqrt{2}$,此时点M为(3+$\sqrt{2}$,-4-$\sqrt{2}$).
点评 本题考查了参数方程,极坐标方程与普通方程的转化,属于基础题.


科目:高中数学 来源: 题型:选择题
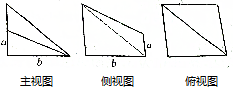
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
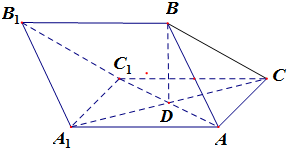 在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com