
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\sqrt{2}$ |
分析 选项结果是固定值,可以利用特殊值验证法,令α,β 分别取0和 $\frac{π}{2}$,再令 α,β 分别取 $\frac{π}{2}$ 和 0,化简可得 tanγ=cotθ,θ+γ=$\frac{π}{2}$,代入要求的式子,化简可得求得结果.
解答 解:令 α=0,β=$\frac{π}{2}$可得 sinγ-cosγ=-sinθ+cosθ ①,
令 α=$\frac{π}{2}$,β=0 可得 cosγ+sinγ=sinθ+cosθ ②,
由①②可得 sinγ=cosθ,cosγ=sinθ,∴tanγ=cotθ,θ+γ=$\frac{π}{2}$,
∴$\frac{{tanθtanγ+cos({θ-γ})}}{{{{sin}^2}({θ+\frac{π}{4}})}}$=$\frac{1+2sinθcosθ}{\frac{1-cos(2θ+\frac{π}{2})}{2}}$=$\frac{2(1+sin2θ)}{1+sin2θ}$=2,
故选:A.
点评 本题考查三角函数的恒等变换及化简求值,求出两个角θ和γ之间的关系,即 tanγ=cotθ,θ+γ=$\frac{π}{2}$,是解题的关键.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 左上方 | B. | 左下方 | C. | 右上方 | D. | 右下方 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
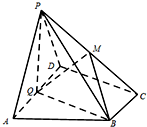 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=$\frac{1}{2}$AD=1,CD=$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com