
分析 (1)求出函数的导数,求得切线的斜率,由条件可得方程,可得n=2,再令导数大于0,得增区间,令导数小于0,得减区间;
(2)由题意可得x2ex>ax+1对x∈(-∞,-1)恒成立,在x<-1时,y=x2ex的图象恒在直线y=ax+1的上方,画出它们的图象,求出x=-1时的交点,通过图象观察即可得到所求范围.
解答 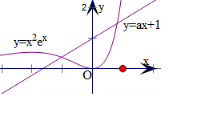 解:(1)f(x)=xnex的导数为f′(x)=(nxn-1+xn)ex,
解:(1)f(x)=xnex的导数为f′(x)=(nxn-1+xn)ex,
由题意可得f′(1)=(n+1)e=3e,
解得n=2,
即有f(x)=x2ex,
导数为f′(x)=(2x+x2)ex,
令f′(x)>0,解得x>0或x<-2,令f′(x)<0,解得-2<x<0,
即有f(x)的增区间为(-∞,-2),(0,+∞),减区间为(-2,0);
(2)f(x)>ax+1对x∈(-∞,-1)恒成立,
即为x2ex>ax+1对x∈(-∞,-1)恒成立,
即有在x<-1时,y=x2ex的图象恒在直线y=ax+1的上方,
画出y=x2ex的图象,直线y=ax+1恒过定点(0,1),
观察x<-1的图象,可得x=-1时,y=$\frac{1}{e}$,此时a=1-$\frac{1}{e}$,
当直线的斜率a≥1-$\frac{1}{e}$时,y=x2ex的图象恒在直线y=ax+1的上方,
故实数a的取值范围是[1-$\frac{1}{e}$,+∞).
点评 本题考查导数的运用:求切线斜率和单调区间,考查不等式恒成立问题,注意运用数形结合的思想方法,属于中档题.


科目:高中数学 来源: 题型:解答题
 如图,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7$\frac{1}{3}$,PO=12,则AB=16.
如图,⊙O的两条割线与⊙O交于A、B、C、D,圆心O在PAB上,若PC=6,CD=7$\frac{1}{3}$,PO=12,则AB=16.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
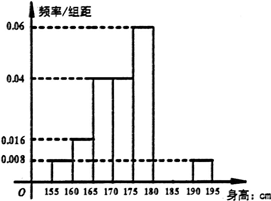 某学校进行体检,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50人身材介于155cm到195cm之间),现将抽取结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],并按此分组绘制如下图所示的频率分布直方图,其中,第六组和第七组还没有绘制完成,已知第一组与第八组人数相同,第七组的人数为3人.
某学校进行体检,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50人身材介于155cm到195cm之间),现将抽取结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],并按此分组绘制如下图所示的频率分布直方图,其中,第六组和第七组还没有绘制完成,已知第一组与第八组人数相同,第七组的人数为3人.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com