Question

11．如图是某日调查部分城市空气质量情况的统计图．

看图回答下面的问题：
（1）空气质量达到优和良的城市共有6个，轻微污染的城市有2个；
（2）轻微污染的城市占所有调查城市的百分之几？
（3）B城市的污染指数比F城市大约高出百分之几？（得数百分号前保留整数）

Answer 1

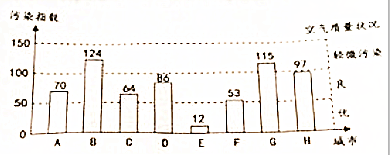
分析 （1）根据空气质量情况统计图中污染指数的大小，得出空气质量达到优和良以及轻微污染的城市个数；
（2）计算轻微污染的城市占所有调查城市的百分比即可；
（3）根据B、F城市的污染指数，计算B城市比F城市污染指数高出的百分比．

解答 解：（1）根据空气质量情况统计图，得；
污染指数低于100的城市有6个，在100～150的有2个，
∴空气质量达到优和良的城市共有6个，轻微污染的城市有2个；
（2）∵$\frac{2}{2+6}$=0.25=25%，
∴轻微污染的城市占所有调查城市的25%；
（3）∵B城市的污染指数是124，F城市的污染指数是53，
∴$\frac{124-53}{53}$≈1.34=134%，
∴B城市比F城市大约高出134%．

点评 本题利用图表法考查了概率与统计的应用问题，也考查了百分比的计算问题，是基础题目．