
 2015年10月4日,强台风“彩虹”登录广东省湛江市,“彩虹”是1949年以来登陆中国陆地的最强台风,“彩虹”给湛江市人民带来了巨大的财产损失,湛江市教育局调查了湛江市50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,作出频率分布直方图,并向全市发出倡议,为受灾的湛江市居民捐款,(视频率为概率)
2015年10月4日,强台风“彩虹”登录广东省湛江市,“彩虹”是1949年以来登陆中国陆地的最强台风,“彩虹”给湛江市人民带来了巨大的财产损失,湛江市教育局调查了湛江市50户居民由于台风造成的经济损失,将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组,作出频率分布直方图,并向全市发出倡议,为受灾的湛江市居民捐款,(视频率为概率)| 经济损失不超过5000元 | 经济损失超过5000元 | 合计 | |
| 捐款超过500元 | 30 | 9 | 39 |
| 捐款不超过500元 | 5 | 6 | 11 |
| 合计 | 35 | 15 | 50 |
分析 (Ⅰ)由题意知X的可能取值为0,1,2,3,且X~B(3,0.06),由此能求出X的分布列和EX.
(Ⅱ)求出K2=4.046>30841,从而得到有95%以上的把握认为捐款数额多于500元和自身经济损失是否超过8000元有关.
解答 解:(Ⅰ)由题意知X的可能取值为0,1,2,3,
由频率分布直方图知损失超过8000元的频率为0.06,用频率表示概率,得X~B(3,0.06),
P(X=0)=${C}_{3}^{0}(0.06)^{0}(1-0.06)^{3}$=0.830584,
P(X=1)=${C}_{3}^{1}(0.06)^{1}(1-0.06)^{2}$=0.159048,
P(X=2)=${C}_{3}^{2}(0.06)^{2}(1-0.06)$=0.010152,
P(X=3)=${C}_{3}^{3}(0.06)^{3}(1-0.06)^{0}$=0.000216,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | 0.830584 | 0.159048 | 0.010152 | 0.000216 |
点评 本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
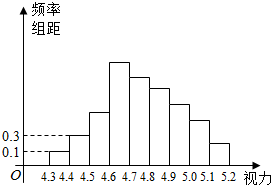 为了解某校学生的视力情况,随机抽查了该校的100名学生,得到如图所示的频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数和为40,后6组的频数和为87,设最大频率a视力在4.5到5.2之间的学生数b,则a,b的值分别为( )
为了解某校学生的视力情况,随机抽查了该校的100名学生,得到如图所示的频率分布直方图,由于不慎将部分数据丢失,但知道前4组的频数和为40,后6组的频数和为87,设最大频率a视力在4.5到5.2之间的学生数b,则a,b的值分别为( )| A. | 0.27,96 | B. | 0.27,83 | C. | 2.7,78 | D. | 2.7,83 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com