
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 类比推理注意二维到三维过程中的变化,平面变立体,面积变体积.
解答 解:我们用圆的性质类比球的性质如下:
①p:圆心与弦(非直径)中点的连线垂直于弦;q:球心与小圆截面圆心的连线垂直于截面,故正确;
②p:与圆心距离相等的两条弦长相等; q:与球心距离相等的两个截面圆的面积相等,故正确;
③p:圆的周长为C=πd(d是圆的直径); q:球的表面积为S=πd2(d是球的直径),故正确;
④p:圆的面积为S=$\frac{1}{2}$R•πd(R,d是圆的半径与直径);q:球的体积为V=$\frac{1}{3}$R•πd2(R,d是球的半径与直径),故正确,
故选:D.
点评 本题考查了类比推理,属于基础题.


科目:高中数学 来源: 题型:解答题
 某地政府调查了工薪阶层1000人的月工资收入,并根据调查结果画出如图所示的频率分布直方图,其中工资收入分组区间是[10,15),[15,20),[20,25),[25,30)[30,35),[35,40](单位:百元)
某地政府调查了工薪阶层1000人的月工资收入,并根据调查结果画出如图所示的频率分布直方图,其中工资收入分组区间是[10,15),[15,20),[20,25),[25,30)[30,35),[35,40](单位:百元)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>c>a | C. | c>b>a | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
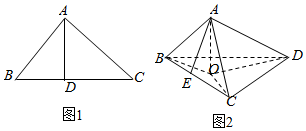 如图1所示,在△ABC中,AB⊥AC,AD⊥BC,则AB2=BD•BC.类似有命题:在三棱锥A-BCD中,如图2所示,AD⊥面ABC.若A在△BCD内的射影为O,E在BC上,且E,O,D在同一条直线上,则S△ABC2=S△BCO•S△BCD,此命题是( )
如图1所示,在△ABC中,AB⊥AC,AD⊥BC,则AB2=BD•BC.类似有命题:在三棱锥A-BCD中,如图2所示,AD⊥面ABC.若A在△BCD内的射影为O,E在BC上,且E,O,D在同一条直线上,则S△ABC2=S△BCO•S△BCD,此命题是( )| A. | 假命题 | |
| B. | 增加AB⊥AC的条件才是真命题 | |
| C. | 真命题 | |
| D. | 增加三棱锥A-BCD是正棱锥的条件才是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 210种 | B. | 180种 | C. | 150种 | D. | 120种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com