
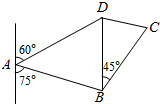
 如图所示B岛在A岛南偏东750方向,距离A岛$4\sqrt{3}$海里,A岛观察所发现在B岛正北方向与A岛的北偏东600方向的交点处D有海上非法走私交易活动,A岛观察人员马上通知在B岛东北方向,距离B岛7海里C处的缉私艇在半小时内赶到D处,求缉私艇的速度至少每小时多少海里?
如图所示B岛在A岛南偏东750方向,距离A岛$4\sqrt{3}$海里,A岛观察所发现在B岛正北方向与A岛的北偏东600方向的交点处D有海上非法走私交易活动,A岛观察人员马上通知在B岛东北方向,距离B岛7海里C处的缉私艇在半小时内赶到D处,求缉私艇的速度至少每小时多少海里? 分析 根据正弦定理和余弦定理结合三角形的边角关系进行求解即可.
解答 解:在△ABD中,∠DAB=180°-600-750=450,
∠ADB=60°,AB=4$\sqrt{3}$,
由正弦定理得:$\frac{AB}{{sin{{60}^0}}}=\frac{BD}{{sin{{45}^0}}}⇒BD=4\sqrt{2}$…(6分)
在△BDC中,$BD=4\sqrt{2},BC=7$,∠DBC=45°,
$DC=\sqrt{B{D^2}+B{C^2}-2×BD•BC•cos{{45}^0}}=5$…(12分)
$v=5÷\frac{1}{2}=10$海里/小时,缉私艇的速度至少每小时10海里.…(14分)
点评 本题主要考查解三角形的应用,根据正弦定理和余弦定理建立方程关系是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $-\frac{2}{3}$ | D. | $-\frac{{\sqrt{5}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}+\frac{y^2}{4}$=1 | B. | $\frac{x^2}{4}+\frac{y^2}{3}$=1 | C. | $\frac{x^2}{16}+\frac{y^2}{9}$=1 | D. | $\frac{x^2}{16}+\frac{y^2}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40$\sqrt{2}$海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=$\frac{\sqrt{26}}{26}$,0°<θ<90°)且与点A相距10$\sqrt{13}$海里的位置C.
在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40$\sqrt{2}$海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45°+θ(其中sinθ=$\frac{\sqrt{26}}{26}$,0°<θ<90°)且与点A相距10$\sqrt{13}$海里的位置C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com