Question

8．直三棱柱ABC-A₁B₁C₁中，∠BAC=90°，AB=BB₁=1，直线B₁C与平面ABC成30°，求点B到平面AC₁的距离及二面角B-CC₁-A的大小．

Answer 1

分析 通过已知条件已知AB=1即为点B到平面AC₁的距离，利用直线B₁C与平面ABC成30°可求得BC，解Rt△ABC即可．

解答 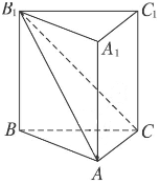解：∵∠BAC=90°，三棱柱ABC-A₁B₁C₁为直三棱柱，
∴AB=1即为点B到平面AC₁的距离，
∠ACB即为二面角B-CC₁-A的平面角，
∵AB=BB₁=1，直线B₁C与平面ABC成30°，
∴∠BCB₁=30°，
∴BC=BB₁•cot30°=$\sqrt{3}$，
∴sin∠ACB=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$，
∴∠ACB=arcsin$\frac{\sqrt{3}}{3}$．

点评 本题考查线面角、二面角，考查解三角形，注意解题方法的积累，属于基础题．