
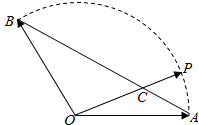
 如图,已知不共线的两个单位向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为120°,点C在线段AB上,设向量$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).
如图,已知不共线的两个单位向量$\overrightarrow{OA}$、$\overrightarrow{OB}$的夹角为120°,点C在线段AB上,设向量$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$(x,y∈R).分析 (1)用$\overrightarrow{OA}$,$\overrightarrow{OB}$表示出$\overrightarrow{AB},\overrightarrow{AC}$,根据A,B,C三点共线得出$\overrightarrow{AB}$=λ$\overrightarrow{AC}$.根据向量的基本定理得出x,y的关系;
(2)计算出$\overrightarrow{OA}•\overrightarrow{OB}$,对$\overrightarrow{OD}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$两边平方得到λ,μ的关系,利用基本不等式得出λ+μ的最大值.
解答 解:(1)$\overrightarrow{AB}$=-$\overrightarrow{OA}$+$\overrightarrow{OB}$,$\overrightarrow{AC}$=$\overrightarrow{OC}-\overrightarrow{OA}$=(x-1)$\overrightarrow{OA}$+y$\overrightarrow{OB}$,
∵A,B,C三点共线,∴存在λ≠0使得$\overrightarrow{AB}$=λ$\overrightarrow{AC}$.
∴$\left\{\begin{array}{l}{(x-1)λ=-1}\\{yλ=1}\end{array}\right.$,两式相加得(x-1)λ+yλ=0,∵λ≠0,∴x+y=1.
(2)$\overrightarrow{OA}•\overrightarrow{OB}$=cos120°=-$\frac{1}{2}$.
∴$\overrightarrow{OD}$2=(λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$)2=λ2+μ2-$\frac{1}{2}λμ$=1.∴λ2+μ2=1+$\frac{1}{2}λμ$≥2λμ,∴λμ≤$\frac{2}{3}$.
∴(λ+μ)2=λ2+μ2+2λμ=1+$\frac{5}{2}λμ$≤$\frac{8}{3}$.
∴λ+μ的最大值为$\frac{2\sqrt{6}}{3}$.
点评 本题考查了平面向量的基本定理,基本不等式的应用,属于基础题.


科目:高中数学 来源: 题型:填空题
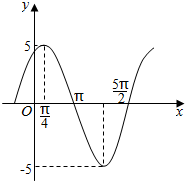 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
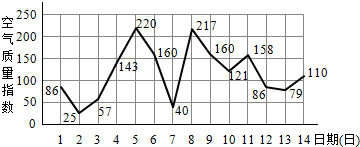 如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).| 空气质量指数 | 污染程度 |
| 小于100 | 优良 |
| 大于100且小于150 | 轻度 |
| 大于150且小于200 | 中度 |
| 大于200且小于300 | 重度 |
| 大于300且小于500 | 严重 |
| 大于500 | 爆表 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com