练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．判断问题是否是排列问题，并说明理由．
    从2，3，5，7，11，13，17，19中任取两个不同的数相除可得多少种不同的结果？

    分析 利用排列的定义，即可得出结论．

    解答 解：由于两数相除，与顺序有关，故属于排列问题．

    点评 本题考查排列的定义，考查学生对概念的理解，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．长时间用手机上网严重影响着学生的健康，如果学生平均每周手机上网的时长超过5小时，则称为“过度用网”．某校为了解A，B两班学生手机上网的情况，分别从这两个班中随机抽取6名同学作为样本进行调查，由样本数据统计得到A，B两班学生“过度用网”的概率分别为$\frac{1}{3}$，$\frac{1}{2}$．
    （1）从A班的样本数据中有放回地抽取2个数据，求恰有1个数据为“过度用网”的概率；
    （2）从A班、B班的样本中各随机抽取2名学生的数据，记“过度用网”的学生人数为ξ，写出ξ的分布列和数学期望Eξ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．复数$\frac{2+i}{1-2i}$=i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．函数f（x）=-3x在区间[1，2]上的最小值是（　　）
    A．-9B．-6C．-3D．-$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．如图，我国南海某处的一个圆形海域上有四个小岛，小岛B与小岛A、小岛C相距都为5n mile，与小岛D相距为$3\sqrt{5}$n mile．小岛A对小岛B与D的视角为钝角，且$sinA=\frac{3}{5}$．
    （Ⅰ）求小岛A与小岛D之间的距离和四个小岛所形成的四边形的面积；
    （Ⅱ）记小岛D对小岛B与C的视角为α，小岛B对小岛C与D的视角为β，求sin（2α+β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

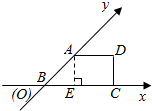    7．有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形，如图所示∠ABC=45°AB=2，AD=1，DC⊥BC，则这块菜地的面积为．（　　）
    A．2+2$\sqrt{2}$B．4+2$\sqrt{2}$C．1+$\sqrt{2}$D．1+$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．从含有8个个体的总体中抽取一个容量为4的样本，则总体中每个个体被抽到的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{6}$D．$\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．甲，乙两人进行射击比赛，每人射击6次，他们命中的环数如下表：
    甲5879106
    乙6741099
    （Ⅰ）根据上表中的数据，判断甲，乙两人谁发挥较稳定；
    （Ⅱ）把甲6次射击命中的环数看成一个总体，用简单随机抽样方法从中抽取两次命中的环数组成一个样本，求该样本平均数与总体平均数之差的绝对值不超过0.5的概率．
    注：$\overline{x}$=$\frac{1}{n}$（x1+x2+…+xn）
    S2=$\frac{1}{n}$[（x1-$\overline{x}$）2+（x2-$\overline{x}$）2+…+（xn-$\overline{x}$）2]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．（1）已知函数f（x）=axekx-1，g（x）=lnx+kx．当a=1时，若f（x）在（1，+∞）上为减函数，g（x）在（0，1）上为增函数，求实数k的值
    （2）已知函数f（x）=x+$\frac{a}{x}$-2lnx，a∈R，讨论函数f（x）的单调区间．

    查看答案和解析>>

    同步练习册答案