
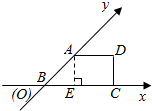
 有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )| A. | 2+2$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{2}$ |
分析 以O点为坐标原点,在直观图中建立平面直角坐标系,按斜二测画直观图的原则,找到四边形ABCD的四个顶点在平面直角坐标系下对应的点,即把直观图中的点还原回原图形中,连结后得到原图形,然后利用梯形面积公式求解.
解答 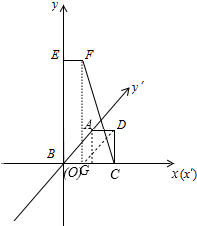 解:如图,
解:如图,
直观图四边形的边BC在x′轴上,在原坐标系下在x轴上,长度不变,
点A在y′轴上,在原图形中在y轴上,且BE长度为AB长的2倍,过E作EF∥x轴,
且使EF长度等于AD,则点F为点D在原图形中对应的点.
∴四边形EBCF为四边形ABCD的原图形.
在直角梯形ABCD中,由AB=2,AD=1,得BC=$\sqrt{2}$+1.
∴四边形EBCF的面积S=$\frac{1}{2}$(EF+BC)•BE=$\frac{1}{2}$(1+$\sqrt{2}$+1)×4=4+2$\sqrt{2}$.
故选:B.
点评 本题考查了水平放置的平面图形的直观图的画法,考查了原图形和直观图面积之间的关系,最好记住结论:$\frac{{S}_{原图}}{{S}_{直观图}}$=2$\sqrt{2}$,该题是基础题


科目:高中数学 来源: 题型:选择题
| A. | 30种 | B. | 35种 | C. | 42种 | D. | 48种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-3) | B. | $({-∞,-\frac{1}{6}})$ | C. | $({-\frac{1}{6},+∞})$ | D. | (-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | V1>V2 | B. | V1<V2 | ||
| C. | V1=V2 | D. | V1,V2无明确大小关系 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com