
分析 由点M($\sqrt{3}$,2)为双曲线C右支上一点,且F2在以线段MF1为直径的圆的圆周上,可得MF2⊥F1F2,进而,求出a,c,即可求出双曲线C的离心率.
解答 解:∵点M($\sqrt{3}$,2)为双曲线C右支上一点,且F2在以线段MF1为直径的圆的圆周上,
∴MF2⊥F1F2,
∴2=$\frac{{b}^{2}}{a}$,
∵$\frac{3}{{a}^{2}}-\frac{4}{{b}^{2}}=1$,
∴a=1,
∴c=$\sqrt{3}$,
∴e=$\frac{c}{a}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查双曲线C的离心率,考查学生的计算能力,确定MF2⊥F1F2,是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
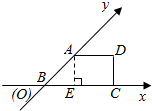 有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )| A. | 2+2$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 5 | 8 | 7 | 9 | 10 | 6 |
| 乙 | 6 | 7 | 4 | 10 | 9 | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(k2>k) | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 3.84 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4x-y+10=0 | B. | 4x-y+2=0 | C. | x-4y+10=0 | D. | x-4y+2=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com