
分析 (Ⅰ)用x,y分别表示小陈、小李到班的时间,则x∈[10,30],y∈[10,30],作出正方形区域得答案;
(Ⅱ)小陈比小李至少晚到5分钟,即x-y≥5,由线性规划知识求出可行域,利用面积比得答案.
解答 解:(Ⅰ)用x,y分别表示小陈、小李到班的时间,
则x∈[10,30],y∈[10,30],
所有可能结果对应坐标平面内一个正方形区域ABCD,
如图所示.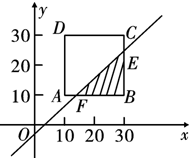
(Ⅱ)小陈比小李至少晚到5分钟,即x-y≥5,
对应区域为△BEF,
所求概率$P=\frac{{{S_{△BEF}}}}{{{S_{ABCD}}}}=\frac{{\frac{1}{2}×15×15}}{20×20}=\frac{9}{32}$.
点评 本题考查几何概型,体现了数学转化思想方法,关键是由题意作出图形,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
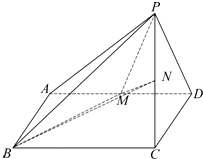 四棱锥P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD为平行四边形,PC⊥平面ABCD,点M,N分别为AD,PC的中点.
四棱锥P-ABCD中,PC=AB=1,BC=2,∠ABC=60°,底面ABCD为平行四边形,PC⊥平面ABCD,点M,N分别为AD,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 243 | B. | $27\root{5}{27}$ | C. | $\sqrt{3}$ | D. | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{2}$ | B. | $\frac{19}{2}$ | C. | 9 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com