
| A�� | ����f��x��=xcosx����f��-x��=-f��x����?x��R�������ƶ�f��x��=xcosxΪ�溯�� | |
| B�� | ��a1=1��an=3n-1�����s1��s2��s3���³�����{an}��ǰn��͵ı���ʽ | |
| C�� | ��Բx2+y2=1�����S=��r2���ƶϣ���Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1�����S=��ab | |
| D�� | ��ƽ�������ε������Ʋ�ռ������������ |

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | A${\;}_{m}^{15}$ | B�� | A${\;}_{m}^{16}$ | C�� | A${\;}_{m+15}^{15}$ | D�� | A${\;}_{m+15}^{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
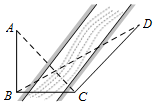 ��ͼ��ij��Ϊ�����Ӷ���AB�ĸߣ���������B�����������ϵĺӰ���ѡһ��C���ڵ�C����õ�A������Ϊ45�㣬���ڵ�C��ƫ��15�㷽��ĺӰ���ѡ��һ��D�����CD�ľ���Ϊ20�ף���BDC=30�㣬����AB�ĸ��ǣ�������
��ͼ��ij��Ϊ�����Ӷ���AB�ĸߣ���������B�����������ϵĺӰ���ѡһ��C���ڵ�C����õ�A������Ϊ45�㣬���ڵ�C��ƫ��15�㷽��ĺӰ���ѡ��һ��D�����CD�ľ���Ϊ20�ף���BDC=30�㣬����AB�ĸ��ǣ�������| A�� | 10�� | B�� | $10\sqrt{2}$�� | C�� | $10\sqrt{3}$�� | D�� | $20\sqrt{3}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1��a��b��0��$��ԲO��x2+y2=b2������Բ��OΪԭ�㣩������ԲC�������ϡ��¶����һ��P��x0��y0����ԲO���������ߣ��е�ֱ�ΪA��B��
��ͼ����֪��ԲC��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1��a��b��0��$��ԲO��x2+y2=b2������Բ��OΪԭ�㣩������ԲC�������ϡ��¶����һ��P��x0��y0����ԲO���������ߣ��е�ֱ�ΪA��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\frac{2}{e}$��1] | B�� | [$\frac{7}{3{e}^{2}}$��1] | C�� | [0��$\frac{2}{e}$] | D�� | [$\frac{7}{3{e}^{2}}$��$\frac{2}{e}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com