
分析 (Ⅰ)已知等式左边利用二倍角的余弦函数公式化简,整理后再利用两角和与差的正弦函数公式及诱导公式化简,利用等差数列性质判断即可得证;
(Ⅱ)利用余弦定理列出关系式,把cosB与b的值代入,利用完全平方公式变形,求出ac的值,再由sinB的值,利用三角形面积公式即可求出所求面积.
解答 解:(Ⅰ)证明:已知等式整理得:a•$\frac{cosC+1}{2}$+c•$\frac{cosA+1}{2}$=$\frac{3b}{2}$,
即a(cosC+1)+c(cosA+1)=3b,
利用正弦定理化简得:sinA(cosC+1)+sinC(cosA+1)=3sinB,
整理得:sin(A+C)+sinA+sinC=3sinB,即sinB+sinA+sinC=3sinB,
∴sinA+sinC=2sinB,
利用正弦定理化简得:a+c=2b,即b-a=c-b,
则a,b,c 成等差数列;
(Ⅱ)∵B=$\frac{π}{3}$,b=4,
∴由余弦定理得:b2=a2+c2-2accosB,
即16=a2+c2-ac=(a+c)2-3ac=4b2-3ac=64-3ac,
整理得:ac=16,
则S△ABC=$\frac{1}{2}$acsinB=4$\sqrt{3}$.
点评 此题考查了正弦、余弦定理,二倍角的余弦函数公式,以及两角和与差的正弦函数公式,熟练掌握定理及公式是解本题的关键.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
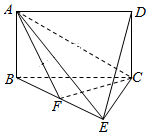 如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.
如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知函数f(x)的定义域为[-2,6],x与f(x)部分对应值如表,f(x)的导函数y=f(x)的图象如图所示.
已知函数f(x)的定义域为[-2,6],x与f(x)部分对应值如表,f(x)的导函数y=f(x)的图象如图所示.| x | -2 | 0 | 5 | 6 |
| f(x) | 3 | -2 | -2 | 3 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | -$\frac{1}{5}$或$\frac{1}{5}$ | C. | -$\frac{3}{4}$或$\frac{3}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 由于f(x)=xcosx满足f(-x)=-f(x)对?x∈R成立,推断f(x)=xcosx为奇函数 | |
| B. | 由a1=1,an=3n-1,求出s1,s2,s3,猜出数列{an}的前n项和的表达式 | |
| C. | 由圆x2+y2=1的面积S=πr2,推断:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的面积S=πab | |
| D. | 由平面三角形的性质推测空间四面体的性质 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com