
分析 (1)由抛物线的焦点坐标,求得c,由a+c=3,则a=2,b2=a2-c2=3,即可求得椭圆的标准方程;
(2)设直线l的方程,代入椭圆方程,利用韦达定理,弦长公式及函数的单调性即可求得△OAB面积S的最大值.
解答 解:(1)由抛物线线上,y2=4x焦点坐标为(1,0),则c=1,
由椭圆C上的点到F的最大距离为a+c=3,则a=2,
b2=a2-c2=3,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)(2)设A(x1,y1),B(x2,y2),直线l的方程为:x=ky+1,
$\left\{\begin{array}{l}{x=ky+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消x,整理得:(3k2+4)y2+6ky-9=0,
∴y1+y2=-$\frac{6k}{3{k}^{2}+4}$,y1y2=-$\frac{9}{3{k}^{2}+4}$,
∴S△OAB=$\frac{1}{2}$×1×|y1-y2|=$\frac{6\sqrt{1+{k}^{2}}}{4+3{k}^{2}}$.
令k2+1=t(t≥1),
S△OAB=$\frac{6\sqrt{1+{k}^{2}}}{4+3{k}^{2}}$=$\frac{6t}{3{t}^{2}+1}$=$\frac{6}{3(t+\frac{1}{3t})}$.
则f(t)=t+$\frac{1}{3t}$,(t≥1),f′(t)=1-$\frac{1}{3{t}^{2}}$=$\frac{3{t}^{2}-1}{3{t}^{2}}$,
∴f(t)在[1,+∞)单调递增,当t=1时,f(t)取最小值,最小值为$\frac{4}{3}$.
S△OAB=$\frac{6}{3(t+\frac{1}{3t})}$(t≥1),的最大值为$\frac{3}{2}$,
∴S△OAB的最大值为$\frac{3}{2}$.
点评 本题主要考查抛物线的应用和抛物线定义,考查直线与椭圆的位置关系的综合应用,椭圆方程的求法,函数的单调性在最值中的应用,考查分析问题解决问题的能力以及计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等 | |
| B. | 如果m⊥n,m⊥α,n∥β,那么α⊥β | |
| C. | 如果α∥β,m?α,那么m∥β | |
| D. | 如果m⊥α,n∥α,那么m⊥n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
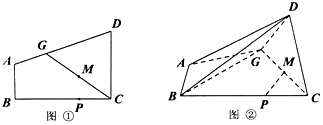
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com