
分析 (Ⅰ) 将直线l的参数方程$\left\{{\begin{array}{l}{x=3-t}\\{y=1+t}\end{array}$消去t参数,可得直线l的普通方程,将ρcosθ=x,ρsinθ=y,ρ2=x2+y2,带入ρ=2$\sqrt{2}$cos(θ-$\frac{π}{4}$)可得曲线C的直角坐标方程.
(Ⅱ)法一:设曲线C上的点为$P({1+\sqrt{2}cosα,1+\sqrt{2}sinα})$,点到直线的距离公式建立关系,利用三角函数的有界限可得最大值.
法二:设与直线l平行的直线为l':x+y+b=0,当直线l'与圆C相切时,得$\frac{{|{1+1+b}|}}{{\sqrt{2}}}=\sqrt{2}$,点到直线的距离公式可得最大值.
解答 解:(Ⅰ) 由直线l的参数方程$\left\{{\begin{array}{l}{x=3-t}\\{y=1+t}\end{array}$消去t参数,得x+y-4=0,
∴直线l的普通方程为x+y-4=0.
由$ρ=2\sqrt{2}cos({θ-&\frac{π}{4}})$=$2\sqrt{2}({cosθcos\frac{π}{4}+sinθsin\frac{π}{4}})=2cosθ+2sinθ$.
得ρ2=2ρcosθ+2ρsinθ.
将ρ2=x2+y2,ρcosθ=x,ρsinθ=y代入上式,
得:曲线C的直角坐标方程为x2+y2=2x+2y,即(x-1)2+(y-1)2=2.
(Ⅱ) 法1:设曲线C上的点为$P({1+\sqrt{2}cosα,1+\sqrt{2}sinα})$,
则点P到直线l的距离为$d=\frac{{|{1+\sqrt{2}cosα+1+\sqrt{2}sinα-4}|}}{{\sqrt{2}}}$=$\frac{{|{\sqrt{2}({sinα+cosα})-2}|}}{{\sqrt{2}}}$=$\frac{{|{2sin({α+\frac{π}{4}})-2}|}}{{\sqrt{2}}}$
当$sin({α+\frac{π}{4}})=-1$时,${d_{max}}=2\sqrt{2}$
∴曲线C上的点到直线l的距离的最大值为$2\sqrt{2}$;
法2:设与直线l平行的直线为l':x+y+b=0.
当直线l'与圆C相切时,得$\frac{{|{1+1+b}|}}{{\sqrt{2}}}=\sqrt{2}$,解得b=0或b=-4(舍去).
∴直线l'的方程为x+y=0.
那么:直线l与直线l'的距离为$d=\frac{{|{0+4}|}}{{\sqrt{2}}}=2\sqrt{2}$
故得曲线C上的点到直线l的距离的最大值为$2\sqrt{2}$.
点评 本题考查点的极坐标和直角坐标的互化,以及利用平面几何知识解决最值问题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行于同一平面的两条直线平行 | B. | 平行于同一直线的两个平面平行 | ||
| C. | 垂直于同一直线的两条直线平行 | D. | 垂直于同一平面的两条直线平行 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 18岁至31岁 | 8 | 12 | 20 | 60 | 140 | 150 |
| 32岁至44岁 | 12 | 28 | 20 | 140 | 60 | 150 |
| 45岁至59岁 | 25 | 50 | 80 | 100 | 225 | 450 |
| 60岁及以上 | 25 | 10 | 10 | 18 | 5 | 2 |
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
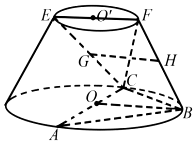 在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′直径,FB是圆台的一条母线.
在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′直径,FB是圆台的一条母线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com