Question

18．如图，在△ABC中，AC=12，∠ABC=2∠C．
（1）若∠C=30°，求△ABC的面积；
（2）若BD平分∠ABC，AH⊥BD于H，求BH的长；
（3）若sin∠C=$\frac{3}{5}$，求sin∠BAC的值．

Answer 1

分析 （1）根据题意推断出∠A=90°，求得两一个直角边，面积可求．
（2）延长BD至E，使得HE=BH证明出BE=AC即可．
（3）求得cosC，进而分别求得sin2C和cos2C，进而利用两角和公式求得答案．

解答 解：（1）∠ABC=2∠C=60°，
∴∠A=90°，AB=$\frac{12}{\sqrt{3}}$=4$\sqrt{3}$
∴△ABC的面积S=$\frac{1}{2}$AB•AC=$\frac{1}{2}$×12×4$\sqrt{3}$=24$\sqrt{3}$．
（2）

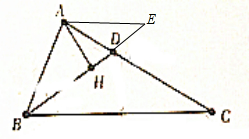
延长BD至E，使得HE=BH；
∵AH⊥BE，且AH平分BE；
∴△BAE是等腰三角形，
∴∠ABE=∠E；
∵BD平分∠ABC交AC于D
∴∠ABE=∠DBC；
∴∠E=∠DBC；
∴AE∥BC；
∴△ADE∽△DBC；
又∵∠ABC=2∠C，BD平分∠ABC交AC于D
∴∠C=∠EBC；
∴BD=DC；
∵△ADE∽△DBC；
∴AD=DE；
∴AC=AD+DC=BD+DE=BE=2BH
∴BH=6．
（3）∵∠ABC=2∠C．
∴∠C＜$\frac{π}{2}$，
∴cosC=$\sqrt{1-si{n}^{2}C}$=$\frac{4}{5}$，
∴sin2C=2sinCcosC=2×$\frac{3}{5}$×$\frac{4}{5}$=$\frac{24}{25}$，
cos2C=cos²c-sin²c=$\frac{16}{25}$-$\frac{9}{25}$=$\frac{7}{25}$．
∴sin∠BAC=sin（π-∠C-2∠C）=sin（∠C+2∠C）=sinCcos2C+cosCsin2C=$\frac{3}{5}$×$\frac{7}{25}$+$\frac{4}{5}$×$\frac{24}{25}$=$\frac{117}{125}$．

点评 本题主要考查了解三角形的相关问题，二倍角公式和两角和公式的运用．考查了学生的推理能力和分析问题的能力．