练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．等比数列 {an}的前n项和为Sn，且a3=2S2+1，a4=2S3+1，则公比q为3．

    分析 a3=2S2+1，a4=2S3+1，两式相减即可得出．

    解答 解：设等比数列 {an}的公比为q，∵a3=2S2+1，a4=2S3+1，
    ∴a4-a3=2a3，化为$\frac{{a}_{4}}{{a}_{3}}$=3=q．
    故答案为：3．

    点评 本题考查了等比数列的定义、递推关系，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

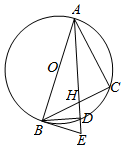    11．如图，圆O的直径为AB且BE为圆O的切线，点C为圆O上不同于A、B的一点，AD为∠BAC的平分线，且分别与BC交于H，与圆O交于D，与BE交于E，连结BD、CD．
    （Ⅰ）求证：∠DBE=∠DBC；
     （Ⅱ）若HE=4，求ED．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．某工厂36名工人的年龄数据如表：
    工人编号  年龄工人编号  年龄工人编号  年龄工人编号  年龄
    1      40
    2      44
    3      40
    4      41
    5      33
    6      40
    7      45
    8      42
    9      43    		10      36
    11      31
    12      38
    13      39
    14      43
    15      45
    16      39
    17      38
    18      36    		19      27
    20      43
    21      41
    22      37
    23      34
    24      42
    25      37
    26      44
    27      42    		28      34
    29      39
    30      43
    31      38
    32      42
    33      53
    34      37
    35      49
    36      39
    （Ⅰ）用系统抽样法从36名工人中抽取容量为9的样本，且在第一分段里用随机抽样法抽到的年龄数据为44，列出样本的年龄数据；
    （Ⅱ）计算（Ⅰ）中样本的平均值$\overline{x}$和方差s2；
    （Ⅲ）求这36名工人中年龄在（$\overline{x}$-s，$\overline{x}$+s）内的人数所占的百分比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知点M，N分别在曲线C1：（x-$\frac{1}{2}$）2+（y-2）2=1和曲线C2：y2=x上运动，那么|MN|的最小值是$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知向量$\overrightarrow{a}$=（2，m+1），$\overrightarrow{b}$=（m+3，4），且（$\overrightarrow{a}$+$\overrightarrow{b}$）∥（$\overrightarrow{a}$-$\overrightarrow{b}$），则m=-5或1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知复数z满足（1+i）z=1（为虚数单位），则z的模为$\frac{\sqrt{2}}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知a，b是正常数，x，y∈（0，+∞），求证：$\frac{a^2}{x}$+$\frac{b^2}{y}$≥$\frac{{{{（a+b）}^2}}}{x+y}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．若函数f（x）=$\left\{\begin{array}{l}{{x}^{2}-2x，x≤2}\\{lo{g}_{a}x-\frac{1}{2}，x＞2}\end{array}\right.$的值域为实数集R，则f（2$\sqrt{2}$）的取值范围是（　　）
    A．（-∞，-$\frac{1}{2}$）B．（-∞，-$\frac{5}{4}$）C．[-$\frac{5}{4}$，+∞）D．[-$\frac{5}{4}$，-$\frac{1}{2}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在△ABC中，a，b，c分别为角A，B，C所对的边．若b=2acosC，则△ABC的形状一定是（　　）
    A．等腰直角三角形B．直角三角形
    C．等腰三角形D．等腰或直角三角形

    查看答案和解析>>

    同步练习册答案