
在Rt△ABC中,CA=CB=2,M,N是斜边AB上的两个动点,且MN=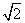 ,则
,则 ·
·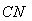 的取值范围为 .
的取值范围为 .
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:
已知函数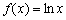 ,
,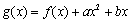 ,其中函数
,其中函数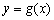 的图象在点
的图象在点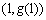 处的切线平行于
处的切线平行于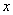 轴.
轴.
(1)确定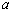 与
与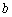 的关系;
的关系;
(2)若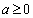 ,试讨论函数
,试讨论函数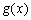 的单调性;
的单调性;
(3)设斜率为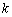 的直线与函数
的直线与函数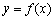 的图象交于两点
的图象交于两点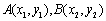
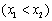 ,求证:
,求证: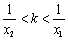 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙、丙三位同学商量高考后外出旅游,甲提议去古都西安,乙提议去海上花园厦门,丙表示随意.最终,三人商定以抛硬币的方式决定结果.规则是:由丙抛掷硬币若干次,若正面朝上,则甲得一分、乙得零分;若反面朝上,则乙得一分、甲得零分,先得4分者获胜.三人均执行胜者的提议.若记所需抛掷硬币的次数为X.
(1)求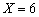 的概率;
的概率;
(2)求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知点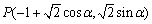 (其中
(其中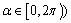 ,点
,点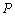 的轨迹记为曲线
的轨迹记为曲线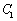 ,以坐标原点为极点,
,以坐标原点为极点,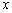 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点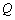 在曲线
在曲线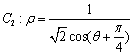 上.
上.
(Ⅰ)求曲线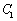 的极坐标方程和曲线
的极坐标方程和曲线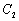 的直角坐标方程;
的直角坐标方程;
(Ⅱ)当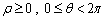 时,求曲线
时,求曲线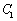 与曲线
与曲线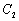 的公共点的极坐标.
的公共点的极坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com