
分析 (1)由题意方程,求得椭圆的焦点坐标,则$\frac{p}{2}=1$,即可求得p的值,求得抛物线方程,利用抛物线的焦点弦公式即可求得|MF|的值;
(2)将直线方程代入抛物线方程,由向量数量积的坐标运算,求得$4{t^2}=λ+\frac{1}{λ}-2$,利用两点之间的距离公式,列方程,即可求得实数λ的值.
解答 解:(1)依题意,椭圆$Γ:\frac{x^2}{2}+{y^2}=1$中,a2=2,b2=1,
故c2=a2-b2=1,F(1,0),
故$\frac{p}{2}=1$,则2p=4,
故抛物线C的方程为y2=4x,
将M(x0,2)代入y2=4x,解得x0=1,
故$|{MF}|=1+\frac{p}{2}=2$.…(4分)
(2)依题意,F(1,0),设l:x=ty+1,设A(x1,y1),B(x2,y2),
联立方程$\left\{\begin{array}{l}{y^2}=4x\\ x=ty+1\end{array}\right.$,消去x,得y2-4ty-4=0.
∴$\left\{\begin{array}{l}{y_1}+{y_2}=4t\\{y_1}{y_2}=-4\end{array}\right.$…①
且$\left\{\begin{array}{l}{x_1}=t{y_1}+1\\{x_2}=t{y_2}+1\end{array}\right.$,又$\overrightarrow{AF}=λ\overrightarrow{FB}$则(1-x1,-y1)=λ(x2-1,y2),即y1=-λy2,代入 ①
得$\left\{\begin{array}{l}({1-λ}){y_2}=4t\\-λy_2^2=-4\end{array}\right.$,…(6分)
消去y2得$4{t^2}=λ+\frac{1}{λ}-2$,且H(-1,0),…(8分)
|HA|2+|HB|2=(x1+1)2+y12+(x2+1)2+y22=x12+x22+2(x1+x2)+2+y12+y22,
=${({t{y_1}+1})^2}+{({t{y_2}+1})^2}+2({t{y_1}+t{y_2}+2})+2+y_1^2+y_2^2$,
=$({{t^2}+1})({y_1^2+y_2^2})+4t({{y_1}+{y_2}})+8$,
=(t2+1)(16t2+8)+4t•4t+8=16t4+40t2+16.
由$16{t^4}+40{t^2}+16=\frac{85}{4}$,…(10分)
解得${t^2}=\frac{1}{8}$或${t^2}=-\frac{21}{8}$(舍),
故λ=2或$\frac{1}{2}$.…(12分)
点评 本题考查抛物线的标准方程及简单几何性质,直线与抛物线的位置关系,向量数量积的坐标运算,两点之间的距离公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{25}$ | B. | $\frac{4π}{25}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2≤0 | B. | $?{x_0}∈R,{x_0}^2>0$ | C. | $?{x_0}∈R,{x_0}^2<0$ | D. | $?{x_0}∈R,{x_0}^2≤0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
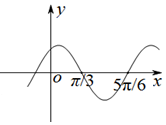 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=sin2x | B. | g(x)=cos2x | C. | $g(x)=sin(2x+\frac{π}{6})$ | D. | $g(x)=sin(2x+\frac{2π}{3})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com