
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{20}$ |
分析 先求出基本事件总数n=${C}_{6}^{3}$=20,再利用列举法求出所取的三个数按一定的顺序可排成等差数列包含的基本事件个数,由此能求出所取的三个数按一定的顺序可排成等差数列的概率.
解答 解:从1、2、3、4、5、6中任取三个数,
基本事件总数n=${C}_{6}^{3}$=20,
所取的三个数按一定的顺序可排成等差数列包含的基本事件有:
(1,2,3),(2,3,4),(3,4,5),(4,5,6),(1,3,5),(2,4,6),
共有6个,
则所取的三个数按一定的顺序可排成等差数列的概率为p=$\frac{6}{20}=\frac{3}{10}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
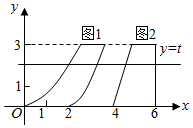 我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为$\frac{9}{2}$.
我国南北朝时代的数学家祖暅提出体积的计算原理(祖暅原理):“幂势既同,则积不容 异”.“势’’即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积恒等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底为l的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图l和图2所截得的两线段长始终相等,则图l的面积为$\frac{9}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
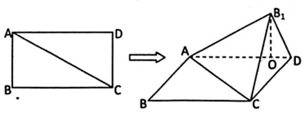
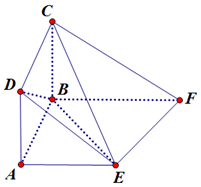 在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角,$AE∥BF,AB=\frac{1}{2}BF=1$,
在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角,$AE∥BF,AB=\frac{1}{2}BF=1$,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 等级 | 1 | 2 | 3 | 4 | 5 |
| 频率 | a | 0.2 | 0.45 | b | c |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com