
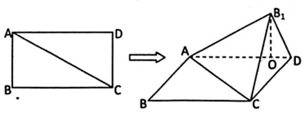
分析 (Ⅰ)利用线面垂直的判定证明AB1⊥CD,又AB1⊥B1C,且B1C∩CD=C,可得AB1⊥平面B1CD;
(Ⅱ)根据体积公式,由已知求得△ABC的面积,而高即为B1O,又易证△AB1D为直角△,则斜边AD上的高B1O可求,则三棱锥B1-ABC的体积可求.
解答 (Ⅰ)证明:如图,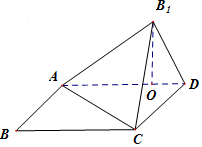
∵ABCD是矩形,∴AB⊥BC,则AB1⊥B1C,
在三棱锥B1-ACD中,∵B1O⊥面ACD,∴B1O⊥CD,
又CD⊥AD,且AD∩B1O=O,∴CD⊥平面AB1O,则CD⊥AB1,
又B1C∩CD=C,∴AB1⊥平面B1CD;
(Ⅱ)解:由于AB1⊥平面B1CD,B1D?平面ABCD,
∴AB1⊥B1D,在Rt△AB1D中,${B}_{1}D=\sqrt{A{D}^{2}-A{{B}_{1}}^{2}}=\sqrt{2}$,
又由B1O•AD=AB1•B1D,得${B}_{1}O=\frac{A{B}_{1}•{B}_{1}D}{AD}$=$\frac{\sqrt{6}}{3}$,
∴${V}_{{B}_{1}-ABC}=\frac{1}{3}$S△ABC•B1O=$\frac{1}{3}×\frac{1}{2}$×1×$\sqrt{3}$×$\frac{\sqrt{6}}{3}$=$\frac{\sqrt{2}}{6}$.
点评 本题考查线面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{27}$=1 | B. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-3,-2,-1,0} | B. | {-2,-1,0} | C. | {-3,-2,-1} | D. | {-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [$\frac{1}{3}$,1] | C. | [$\frac{1}{2}$,$\frac{2}{3}$] | D. | [$\frac{1}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 非一线 | 一线 | 总计 | |
| 愿生 | 45 | 20 | 65 |
| 不愿生 | 13 | 22 | 35 |
| 总计 | 58 | 42 | 100 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关” | |
| C. | 有99%以上的把握认为“生育意愿与城市级别有关” | |
| D. | 有99%以上的把握认为“生育意愿与城市级别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{25}$ | B. | $\frac{4π}{25}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com