
分析 根据模的取值范围,得到4≤|$\overrightarrow{a}$-$\overrightarrow{b}$|2≤36,4≤|$\overrightarrow{a}$|2、|$\overrightarrow{b}$|2≤36,再根据|$\overrightarrow{a}$-$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2$\overrightarrow{a}$•$\overrightarrow{b}$即可求出答案.
解答 解:∵|$\overrightarrow{a}$|、|$\overrightarrow{b}$|、|$\overrightarrow{a}$-$\overrightarrow{b}$|∈[2,6],
∴4≤|$\overrightarrow{a}$-$\overrightarrow{b}$|2≤36,4≤|$\overrightarrow{a}$|2、|$\overrightarrow{b}$|2≤36
∴-36≤-|$\overrightarrow{a}$|2、-|$\overrightarrow{b}$|2≤-4
∴4≤|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-2$\overrightarrow{a}$•$\overrightarrow{b}$≤36,
∴-68≤-2$\overrightarrow{a}$•$\overrightarrow{b}$≤28,
∴-14≤$\overrightarrow{a}$•$\overrightarrow{b}$≤34,
∴$\overrightarrow{a}$•$\overrightarrow{b}$∈[-14,34],
故答案为:[-14,34]
点评 本题考查了向量的数量积公式和向量和不等式的性质,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | {-3,-2,-1,0} | B. | {-2,-1,0} | C. | {-3,-2,-1} | D. | {-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| y1 | 5 | 130 | 505 | 1130 | 2005 | 3130 | 4505 |
| y2 | 5 | 94.478 | 1785.2 | 33733 | 6.37×105 | 1.2×107 | 2.28×108 |
| y3 | 5 | 30 | 55 | 80 | 105 | 130 | 155 |
| y4 | 5 | 2.3107 | 1.4295 | 1.1407 | 1.0461 | 1.0151 | 1.005 |
| A. | y2、y1 | B. | y2、y3 | C. | y4、y3 | D. | y1、y3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{25}$ | B. | $\frac{4π}{25}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
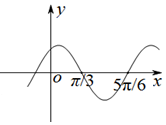 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=sin2x | B. | g(x)=cos2x | C. | $g(x)=sin(2x+\frac{π}{6})$ | D. | $g(x)=sin(2x+\frac{2π}{3})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com