
分析 构造数列{$\frac{{a}_{n}}{n}$},从而可证明其为以1为首项,1为公差的等差数列,从而求得an=n2,Sn=$\frac{n(n+1)(2n+1)}{6}$,从而化简$\frac{{S}_{n}}{n}$-$\frac{1}{2}$an=$\frac{-{n}^{2}+3n+1}{6}$;从而利用二次函数求最值点.
解答 解:∵an+1=$\frac{n+1}{n}$an+n+1,
∴$\frac{{a}_{n+1}}{n+1}$=$\frac{{a}_{n}}{n}$+1,
∴$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=1,
又∵$\frac{{a}_{1}}{1}$=1,
∴数列{$\frac{{a}_{n}}{n}$}是以1为首项,1为公差的等差数列,
故$\frac{{a}_{n}}{n}$=1+n-1=n,
故an=n2,Sn=$\frac{n(n+1)(2n+1)}{6}$,
故$\frac{{S}_{n}}{n}$-$\frac{1}{2}$an=$\frac{(n+1)(2n+1)}{6}$-$\frac{1}{2}$n2
=$\frac{-{n}^{2}+3n+1}{6}$;
∵y=-x2+3x+1的图象开口向下,且对称轴为x=$\frac{3}{2}$;
∴当n=1或n=2时,$\frac{{S}_{n}}{n}$-$\frac{1}{2}$an取最大值,
故答案为:1或2.
点评 本题考查了数列的性质的判断与应用,同时考查了转化思想与函数思想的应用及构造法的应用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{28\sqrt{7}}{3}$π | B. | 28$\sqrt{7}$π | C. | $\frac{32}{3}$π | D. | 4$\sqrt{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.55 | B. | 0.6 | C. | 0.65 | D. | 0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
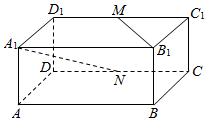 长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )| A. | $\frac{\sqrt{30}}{10}$ | B. | 0 | C. | $\frac{\sqrt{15}}{10}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:
中国传统文化中很多内容体现了数学的对称美,如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分展现了相互转化、对称统一的形式美、和谐美.给出定义:能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”.给出下列命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m?β,则α∥β | B. | 若m∥α,m∥β,则α∥β | C. | 若m⊥α,m∥β,则α⊥β | D. | 若m⊥α,m⊥β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
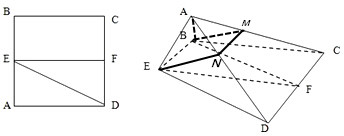 已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.
已知正方形ABCD,E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com