Question

7．已知F₁，F₂是椭圆和双曲线的公共焦点，P是它们的一个公共点，且$∠{F_1}P{F_2}=\frac{π}{2}$，椭圆和双曲线的离心率分别为e₁、e₂，则$\frac{1}{{{e_1}^2}}+\frac{1}{{{e_2}^2}}$=2．

Answer 1

分析 先设椭圆的长半轴长为a₁，双曲线的半实轴长a₂，焦距2c．因为涉及椭圆及双曲线离心率的问题，所以需要找a₁，a₂，c之间的关系，而根据椭圆及双曲线的定义可以用a₁，a₂表示出|PF₁|，|PF₂|并且，$∠{F_1}P{F_2}=\frac{π}{2}$，在△F₁PF₂中根据勾股定理可得到：，${{a}_{1}}^{2}+{{a}_{1}}^{2}=2{c}^{2}$该式可变成：$\frac{1}{{{e_1}^2}}+\frac{1}{{{e_2}^2}}$=2．

解答 解：如图，设椭圆的长半轴长为a₁，双曲线的半实轴长为a₂，则根据椭圆及双曲线的定义：
得|PF₁|+|PF₂|=2a₁+a₂，∴|PF₁|-||PF₂|=2a₂
∴|PF₁|=a₁+a₂，|PF₂|=a₁-a₂，设|F₁F₂|=2c，∠F₁PF₂=$\frac{π}{2}$，
在△PF₁F₂中由勾股定理得，4c²=（a₁+a₂）²+（a₁-a₂）²
∴化简得：${{a}_{1}}^{2}+{{a}_{1}}^{2}=2{c}^{2}$该式可变成：$\frac{1}{{{e_1}^2}}+\frac{1}{{{e_2}^2}}$=2．
故答案为：2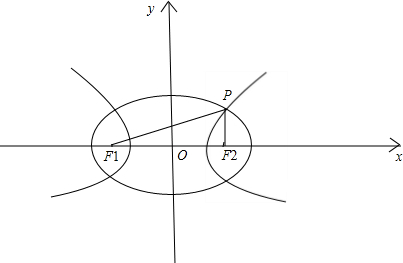

点评 考查椭圆及双曲线的交点，及椭圆与双曲线的定义，以及它们离心率的定义，属于基础题．