
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
分析 把直线y=kx-1方程代入曲线x2-y2=4,化为:(k2-1)x2-2kx+5=0,由△=0,解得k=$±\frac{\sqrt{5}}{2}$.此时直线与双曲线有唯一公共点.当k=±1时,直线y=kx-1与曲线x2-y2=4仅有一个公共点.j即可判断出结论.
解答 解:把直线y=kx-1方程代入曲线x2-y2=4,化为:(k2-1)x2-2kx+5=0,由△=4k2-20(k2-1)=0,解得k=$±\frac{\sqrt{5}}{2}$.此时直线与双曲线有唯一公共点.
当k=±1时,直线y=kx-1与曲线x2-y2=4仅有一个公共点.
∴$k=±\frac{{\sqrt{5}}}{2}$是直线y=kx-1与曲线x2-y2=4仅有一个公共点的充分不必要条件.
故选:A.
点评 本题考查了直线与双曲线的交点与判别式的关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},2)$ | B. | (2,+∞) | C. | (1,2) | D. | $(\frac{1}{2},1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | 5 | C. | 90 | D. | 180 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1) | B. | (0,1) | C. | $({1,\sqrt{2}})$ | D. | (-∞,-2)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
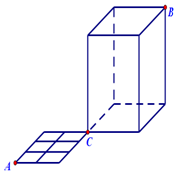 如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有( )条.
如图,一只蚂蚁从点A出发沿着水平面的线条爬行到点C,再由点C沿着置于水平面的长方体的棱爬行至顶点B,则它可以爬行的不同的最短路径有( )条.| A. | 40 | B. | 60 | C. | 80 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | -2 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com