
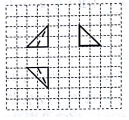
 如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )
如图所示,网格纸上每个小格都是边长为1的正方形,粗线画出的是一个几何体的三视图,则该几何体的表面积为( )| A. | 2+2$\sqrt{3}$+$\sqrt{6}$ | B. | 4+2$\sqrt{3}$+$\sqrt{6}$ | C. | 4+4$\sqrt{3}$+$\sqrt{6}$ | D. | 2+$\sqrt{3}$+$\sqrt{6}$ |
分析 由三视图可知:该几何体为三棱锥P-ABC,其中侧面PAB⊥底面ABC,在平面PAB内,过点P作PD⊥AB,垂足为D,连接CD,CD⊥AD.进而得出.
解答 解:由三视图可知:该几何体为三棱锥P-ABC,
其中侧面PAB⊥底面ABC,在平面PAB内,过点P作PD⊥AB,垂足为D,连接CD,CD⊥AD.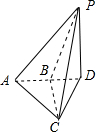
该几何体的表面积S=$\frac{1}{2}×1×2$×2+$\frac{\sqrt{3}}{4}×(2\sqrt{2})^{2}$+$\frac{1}{2}×2\sqrt{2}×\sqrt{3}$
=2+2$\sqrt{3}$+$\sqrt{6}$.
故选:A.
点评 本题考查了三棱锥是三视图、三角形面积计算公式,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\frac{5}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+3y-12=0 | B. | 2x+3y+12=0 | C. | 2x-3y+12=0 | D. | 2x-3y-12=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 选修课程 | 线性代数 | 微积分 | 大学物理 | 商务英语 | 文学写作 | 合计 |
| 选课人数 | 180 | x | 120 | y | 60 | 600 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{9}{10}$x | B. | y=±$\frac{10}{9}$x | C. | y=±$\frac{{3\sqrt{10}}}{10}$x | D. | y=±$\frac{{\sqrt{10}}}{3}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com